Like & Unlike Fractions Addition Calculator
Fractions Addition - work with steps
Input Data :
Fraction A = `2/3`
Fraction B = `3/2`
Objective :
Find what is fraction addition for given input data?
Solution :
A + B = `2/3 + 3/2`
denominator of the two fraction is different. Therefore, find lcm for two denominators (3, 2) = 6
Multiply lcm with both numerator & denominator
`2/3 + 3/2 = (2\times6)/(3\times6) + (3\times6)/(2\times6)`
= `(2\times2)/(6) + (3\times3)/(6)`
= `(4)/(6) + (9)/(6)`
Add two numerator of the fraction
`(4)/(6) + (9)/(6) = (4 + 9)/6 = 13/6`
`2/3+3/2 = 13/6`
Fractions addition calculator uses two proper or improper fractions, `frac{a}{b}` and `frac{c}{d}` for `b, d ne 0` and calculates their sum.
It is an online tool for finding the sum in the simplest form of two proper or improper fractions.
It is necessary to follow the next steps:
- Enter two fractions `a/b` and `c/d` in the box. The numbers `a,b,c` and `d` must be integers such that `b` and `d` must be nonzero.
- Press the "GENERATE WORK" button to make the computation;
- Fractions addition calculator will give the sum of two numbers represented as fractions.
Output:A fraction in the simplest form.
Fractions Addition Rule:
The sum of two fractions `a/b` and `c/d` is determined by the following formula
- If denominators are equal, `b = d`: $$\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b},\quad \mbox{for}\;b\ne0$$
- If denominators are different, `b\ne d`:
$$\frac{a}{b}+\frac{c}{d}=\frac{a\times d+c\times b}{b\times d},\quad \mbox{for}\;b,d\ne0$$
or equivalently,$$\frac{a}{b}+\frac{c}{d}=\frac{a\times \frac{LCM(b,d)}{b}+c\times \frac{LCM(b,d)}{d}}{LCM(b,d)},\quad \mbox{for}\;b,d\ne0$$
where `LCM(b,d)` is the least common multiple of `b` and `d`.
How to Add Fractions?
Fractions addition calculator is an online tool to find the sum of two regular or irregular fractions in fraction & decimal form. Refer the example calculations to know how to add two fractions with same or different denominators.
- When denominators are equal
When denominators of fractions are equal, then their sum will be the sum of numerators over the common denominator. If necessary, the result may be simplified. This can be expressed algebraically:
$$\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b},\quad \mbox{for}\;b\ne0$$ - When denominators are different
When denominators of fractions are different, to add two or more such fractions, it is necessary to follow the next steps:- Find the LCM of denominators;
- Rewrite the fractions over the LCM;
- Add new numerators;
- The result is the sum of numerators over the LCM;
- Simplify the result if needed.
$$\frac{a}{b}+\frac{c}{d}=\frac{a\times \frac{LCM(b,d)}{b}+c\times \frac{LCM(b,d)}{d}}{LCM(b,d)},\quad \mbox{for}\;b,d\ne0$$
If `LCM(b,d)=b\times d`, then the previous formula becomes
$$\frac{a}{b}+\frac{c}{d}=\frac{a\times d+c\times b}{b\times d},\quad \mbox{for}\;b,d\ne0$$
For example, let us find the sum for `\frac {2}{3}` and `\frac {3}{2}`. Since `LCM(3,2)=3\times 2`, then$$\frac 23+\frac 32=\frac {2\times 2+3\times 3}{3\times 2}=\frac {13}6$$
To write the sum in simplest form, find the GCF of the numerator and denominator of the sum. Because `13` and `6` are relatively prime numbers, the final result is `\frac{13}{6}`.
The similar consideration can be applied in addition of algebraic fractions.
The similar consideration can be applied in addition of algebraic fractions.
The Fractions Addition work with steps shows the complete step-by-step calculation for finding the sum of two fractions `\frac{2}{3}` and `\frac{3}{2}` using the fractions addition rule. For any other fractions, just supply two proper or improper fractions and click on the "GENERATE WORK" button. The grade school students may use this adding two like or unlike fractions calculator to generate the work, verify the results of adding two or more numbers derived by hand or do their homework problems efficiently.
Real World Problems Using Fractions Addition
The problem of adding two or more fractions can be found in almost all spheres of life and science. The addition of fractions can be represented by area model.
For example, let us find the sum `\frac 3 5+\frac 1 6`.
If we divide a square into five congruent rectangles, `\frac 3 5` means `3` rectangles of the square.
If we divide the same square into `30` rectangles `18` shared rectangles have equal area as `3` previously shared rectangles. So, `\frac 3 5` is equal to `\frac {18} {30}`.
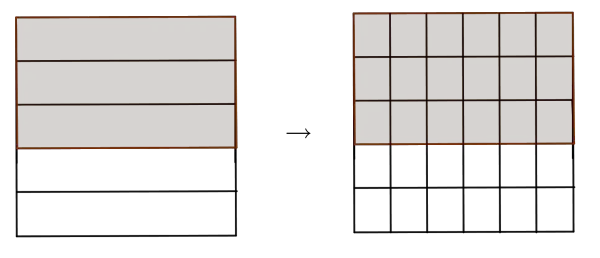
In the same manner, we can rewrite the fraction `1/6` as `5/30`.

Since both fractions have the same common denominator, we can add the fractions. If we add rectangles on the first picture to the rectangle on the second picture, we get a total of `23` rectangles. So, the result is `23/30`.

Fraction Addition Practice Problems
Practice Problem 1:
To make a cake, we need `7/8` of a cap of white sugar and `4/5` a cap of brown sugar. How much sugar do we need to make this cake?
Practice Problem 2:
John ate `2/5` of pizza and Sarah ate `3/11` of the same pizza. How much did they eat together?
The like and unlike fractions addition calculator, formula, step by step calculation, real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the addition of two or more numbers represented as fractions. Using this concept they can be able to solve complex real world algebraic problems and equations.
| Like & Unlike Fractions Addition | |
|---|---|
| Fractions | Sum |
| 1/7 + 7/8 | 57/56 |
| 2/9 + 1/8 | 25/72 |
| 1/7 + 5/9 | 44/63 |
| 1/6 + 1/5 | 11/30 |
| 2/7 + 1/6 | 19/42 |
| 4/3 + 3/7 | 37/21 |
| 6/7 + 2/9 | 68/63 |
| 3/8 + 2/3 | 25/24 |
| 9/5 + 4/5 | 13/5 |
| 6/7 + 7/3 | 67/21 |
| 9/8 + 1/6 | 31/24 |
| 7/4 + 9/7 | 85/28 |
| 5/2 + 3/7 | 41/14 |
| 2/5 + 1/5 | 3/5 |
| 7/9 + 4/3 | 19/9 |
| 1/7 + 7/4 | 53/28 |
| 3/5 + 2/5 | 1/1 |
| 5/2 + 5/3 | 25/6 |
| 7/2 + 8/3 | 37/6 |
| 1/9 + 8/9 | 1/1 |
| 7/5 + 2/7 | 59/35 |
| 2/9 + 2/5 | 28/45 |
| 4/7 + 5/6 | 59/42 |
| 4/5 + 2/3 | 22/15 |
| 1/8 + 1/8 | 1/4 |
| 1/4 + 9/8 | 11/8 |
| 9/5 + 9/7 | 108/35 |
| 2/7 + 2/9 | 32/63 |
| 4/7 + 1/2 | 15/14 |
| 9/7 + 7/4 | 85/28 |
| 5/8 + 5/4 | 15/8 |
| 2/3 + 5/9 | 11/9 |
| 3/8 + 5/3 | 49/24 |
| 7/5 + 1/8 | 61/40 |
| 1/4 + 1/8 | 3/8 |
| 8/3 + 8/3 | 16/3 |
| 7/4 + 4/9 | 79/36 |
| 3/2 + 3/2 | 3/1 |
| 6/5 + 9/4 | 69/20 |
| 9/8 + 1/4 | 11/8 |
| 5/3 + 1/6 | 11/6 |
| 3/4 + 5/2 | 13/4 |
| 1/4 + 8/7 | 39/28 |
| 5/2 + 1/5 | 27/10 |
| 8/7 + 9/5 | 103/35 |
| 4/3 + 2/9 | 14/9 |
| 3/8 + 5/8 | 1/1 |
| 7/6 + 8/7 | 97/42 |
| 7/9 + 1/9 | 8/9 |
| 1/8 + 4/3 | 35/24 |
| 1/3 + 4/5 | 17/15 |
| 8/9 + 2/3 | 14/9 |
| 4/3 + 1/5 | 23/15 |
| 7/9 + 7/8 | 119/72 |
| 8/5 + 7/3 | 59/15 |
| 3/5 + 1/4 | 17/20 |
| 7/5 + 4/5 | 11/5 |
| 4/9 + 5/6 | 23/18 |
| 3/5 + 8/9 | 67/45 |
| 3/4 + 3/8 | 9/8 |
| 3/7 + 9/4 | 75/28 |
| 3/4 + 9/4 | 3/1 |
| 7/4 + 4/3 | 37/12 |
| 5/2 + 7/8 | 27/8 |
| 7/9 + 9/5 | 116/45 |
| 7/3 + 2/5 | 41/15 |
| 9/5 + 7/5 | 16/5 |
| 2/7 + 4/7 | 6/7 |
| 5/3 + 6/7 | 53/21 |
| 2/5 + 4/7 | 34/35 |
| 3/5 + 3/2 | 21/10 |
| 1/5 + 5/7 | 32/35 |
| 3/5 + 8/7 | 61/35 |
| 1/4 + 8/9 | 41/36 |
| 2/7 + 2/5 | 24/35 |
| 3/8 + 8/5 | 79/40 |
| 1/5 + 1/7 | 12/35 |
| 5/9 + 2/5 | 43/45 |
| 2/7 + 4/3 | 34/21 |
| 5/8 + 3/7 | 59/56 |
| 2/9 + 1/5 | 19/45 |
| 6/5 + 5/8 | 73/40 |
| 7/5 + 3/2 | 29/10 |
| 6/5 + 5/7 | 67/35 |
| 7/5 + 5/7 | 74/35 |
| 8/9 + 1/8 | 73/72 |
| 8/9 + 5/9 | 13/9 |
| 7/4 + 7/5 | 63/20 |
| 2/9 + 9/7 | 95/63 |
| 6/5 + 7/3 | 53/15 |
| 5/3 + 9/4 | 47/12 |
| 2/5 + 3/5 | 1/1 |
| 6/5 + 1/9 | 59/45 |
| 6/5 + 3/4 | 39/20 |
| 1/6 + 9/7 | 61/42 |
| 2/3 + 4/5 | 22/15 |
| 3/2 + 5/7 | 31/14 |
| 6/7 + 3/5 | 51/35 |
| 5/9 + 5/2 | 55/18 |
| 7/2 + 9/7 | 67/14 |

