Fractions Division Calculator

Fractions division calculator uses two proper or improper fractions, `a/b` and `c/d` such that `b,c,d\ne0`, and calculates the quotient for `a/b` divided by `c/d`. It is an online tool to find the quotient in the simplest form of two proper or improper fractions.
It is necessary to follow the next steps:

1. Enter two fractions, the dividend `a/b` and the divisor `c/d` in the box. The numbers `a, b, c` and `d` must be integers such that `b, c` and `d` must be nonzero.
2. Press the "GENERATE WORK" button to make the computation;
3. Fractions division calculator will give the quotient of two numbers represented as fractions.

Input :Two fractions;
Output :A fraction in the simplest form

Fractions Division Rule: The quotient for the fraction `a/b` divided by `c/d`, for `b,c,d\ne0`, is determined by the following formula

How to Divide a Fraction by a Fraction?

Division of fractions (or any other numbers or variables) may be indicated either by a division signs `\div` or `:` between two fractions or by writing the division in the form of the complex fraction. A complex fraction is a fraction where the numerator, denominator, or both contain a fraction. So, division of fractions can be represented as in the following examples:

The first fraction, in this case `2/3`, is the dividend, the second fraction, in this case `5/4`, is the divisor, and the result is the quotient.
One property of fractions that do not valid for whole numbers and integers is well known as inverse property of fractions. Two fractions whose product is `1` are called multiplicative inverses or reciprocal.This means, if `\frac ab\times \frac cd=1` for `b,d\ne0`, then `\frac{a}{b}` and `\frac{c}{d}` are reciprocal. The product of a number and its reciprocal is `1`. In other words, for every fraction `frac ab`, where `a, b \ne0`, there is exactly one number `\frac b a` such that $$\frac ab\times \frac ba=1$$
For example, `5/7` and `7/5` are reciprocal because `\frac {5}{7}\times \frac {7}{5}=1.`
When we deal with dividing fractions, there are some important cases which deserve to be mentioned here:
Division of a fraction by another fraction
Dividing by the fraction $\frac c d$ is equal to the multiplying by the fraction `\frac d c`, its reciprocal. This is valid for any fraction. Hence, to divide `a/b` by `c/d` multiply `a/b` by `d/c`, i.e. multiply their numerators and multiply their denominators. In other words, the quotient of two fractions `a/b` and `c/d` for `b,c,d\ne0` is To summarize, to find the quotient of two fractions, it is necessary to follow three steps:

1. Find the reciprocal of the divisor
2. Multiply the dividend by this reciprocal
3. Simplify the product if needed.

For example, let us divide the fractions: `8/3\divide7/2`. Using the division rule explained above, we obtain
$$\frac{8}{3}\div\frac{7}{2}=\frac{8}{3}\times\frac{2}{7}=\frac{8\times2}{3\times7}=\frac{16}{21}$$
To write the quotient in simplest form, find the GCF of the numerator and denominator of the quotient. Since 16 and 21 are relatively prime numbers, the GCF of 16 and 21 is 1. So, the quotient for fraction `\frac{8}{3}` divided by `\frac{7}{2}` is `\frac{16}{21}`

Division of a fraction by a whole number
Since a whole number can be rewritten as itself divided by $1$, we can apply the previous rule of division of a fraction by another fraction. The quotient for the fraction `\frac{a}{b},b\ne0` divided by the whole number `c, c\ne0`, is the product of `\frac{a}{b}` and `\frac 1 c`, the reciprocal of `c`. This can be written in the following way
$$\frac a b\div c=\frac a b\times \frac{1}{c}$$
Division of a fraction by a mixed numbers
Firstly, it is necessary to convert the mixed number to improper fractions then divide the fractions. For example, find `\frac{3}{4}\div3\frac {1}{3}`. Since `3\frac{1}{3}` is equal to `\frac{10}{3}`, the quotient for the fraction `\frac{3}{4}` divided by the mixed number `3\frac {1}{3}` is equal to the quotient for the fraction `\frac{3}{4}` divided by the fraction `\frac {10}3`. Then we will continue with the rule for division of a fraction by another fraction.

The similar consideration can be applied in the division of algebraic fractions.

The Fractions Division work with steps shows the complete step-by-step calculation for finding quotient for the fraction `\frac{8}{3}` divided by `\frac{7}{2}` using the division rule. For any other fractions, just supply two proper or improper fractions and click on the "GENERATE WORK" button. The grade school students may use this fraction division calculator to generate the work, verify the results of dividing numbers derived by hand or do their homework problems efficiently.

Real World Problems Using Fraction Division

Fractions division is useful in dimensional analysis. Dimensional analysis is the process of including units of measurement in division. For example, how many uniforms can be made with `a/b` meters of factory if each uniform requires `c/d` meter.

For fractions with small numerators and denominators, an area model is very useful to check or derive result of fractions division. Let us explain this concept thought example `1/2 \divide 3/4` . Firstly, divide two squares to represent each fractions and shade the corresponding their parts. This is illustrated by the following picture:

Then we will redraw both squares to have the same dimension

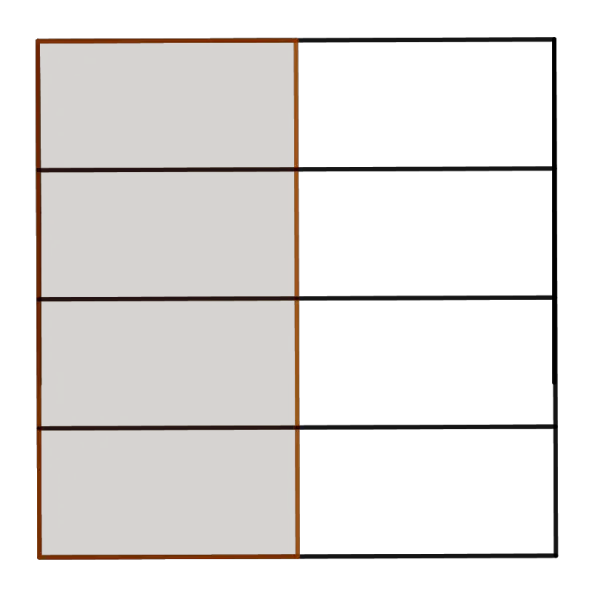
The quotient for the fraction `1/2` divided by `3/4` is the total number of shaded rectangles in the first square to the shaded rectangles in the second square, i.e. `4/6`.

Fraction Division Practice Problems

Practice Problem 1:
Divide `123/x` by `9/x^2` and write the result in the simplest form.

Practice Problem 2:
Ann for `5/2` hours earns `$10.5.` What is the hourly rate?

Practice Problem 3:
How many groups of `2/7` are in `1/2`.

The fractions division calculator, formula, step by step calculation, real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the division of two or more numbers represented as fractions. Using this concept they can be able to solve complex real world algebraic problems and equations.