LCM Calculator
LCM of Numbers - work with steps
Input Data :
Data set = 5, 20, 40, 80, 100
Number of elements = 5
Objective :
Find the LCM of given integers?
Solution :
Find Prime factor for each input
5 = 5 = 5
20 = 2 x 2 x 5 = 22 x 5
40 = 2 x 2 x 2 x 5 = 23 x 5
80 = 2 x 2 x 2 x 2 x 5 = 24 x 5
100 = 2 x 2 x 5 x 5 = 22 x 52
The Product of all factors with highest powers
LCM = 24 x 52 = 2 x 2 x 2 x 2 x 5 x 5
LCM = 400
LCM calculator uses two or more numbers and calculates the least common multiple, i.e. the smallest positive integer which is divisible by each one of these numbers. It is an online mathematical tool specially programmed to find out the LCM of two or more integers.
It is necessary to follow the next steps:
- Enter two or more numbers in the box. These numbers must be integers and may be separated by commas. The values can be copied from a text document or a spreadsheet;
- Press the "GENERATE WORK" button to make the computation;
- LCM calculator will give the least common multiple of two or more numbers.
Output : The least common multiple is an integer number.
The LCM calculator determines the least common multiple of two or more integers using the prime factorization.
| Integers | LCM |
|---|---|
| LCM of 9 and 4 | 36 |
| LCM of 3 and 7 | 21 |
| LCM of 9 and 12 | 36 |
| LCM of 8 and 7 | 56 |
| LCM of 3 and 8 | 24 |
| LCM of 9 and 6 | 18 |
| LCM of 12 and 8 | 24 |
| LCM of 3 and 9 | 9 |
| LCM of 8 and 32 | 32 |
| LCM of 24 and 36 | 72 |
| LCM of 22 and 36 | 396 |
| LCM of 36 and 27 | 108 |
| LCM of 21 and 63 | 63 |
| LCM of 12 and 20 | 60 |
| LCM of 24 and 8 | 24 |
| LCM of 12 and 15 | 60 |
| LCM of 18 and 12 | 36 |
| LCM of 21 and 12 | 84 |
| LCM of 12 and 42 | 84 |
What is Least Common Multiple?
A multiple of some number is a product of that number and a whole number. For example, multiples of $3$ are: $0,3,6,9,\ldots$
Sometimes numbers have some of the same multiples, well known as common multiple. The least of the nonzero common multiples is called the least common multiple (LCM for short). The least common multiple is also known as the lowest common multiple or smallest common multiple.
The least common multiple of two integers $x$ and $y$ is usually denoted by $LCM(x,y)$ or $[x,y].$ In other words, it is the smallest positive integer that is divisible by both numbers $x$ and $y$.
Since division by zero is undefined, then $x$ and $y$ are both nonzero numbers. In some literature, it is defined $LCM(x,0)=0$, for all $x$, but we will require that the numbers $x$ and $y$ are both nonzero numbers.
Two numbers are relatively prime or coprime if their only common factor is $1$. So, the least common multiple of the two relatively prime numbers $x$ and $y$ is their product $x\times y$. If one number is prime, for example $x$, and the prime factors of the second number $y$ include the number $x$, then the LCM of these numbers is $y$.
How to Calculate Least Common Multiple?
There are several methods for finding LCM of two integers. The same procedures can be applied to more than two integers. For example, let us find the LCM of $54$ and $36$.
- Using prime factorization.
The prime factors of these numbers are $2$ and $3$. By multiplying the greatest power of $2$ and $3$ form these factorizations, the LCM is ${\color{blue}2^2\times3^3}=108$.
The fundamental theorem of arithmetic states that every integer greater than $1$ can be factored uniquely into primes (Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 3 and 21, 1979.). For instance, $54$ can be factored uniquely into $2\times3\times 3\times 3$, i.e. there is no other product of primes equal to $54$.
- Venn diagram.

- Factor Trees.
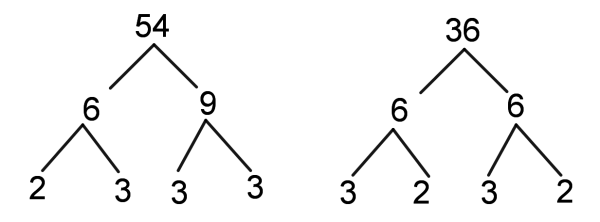
A factor tree can also be used to find the LCM. The picture above represents the factor trees for the numbers $54$ and $36$. Firstly, we should identify any shared primes, in this case the shared primes are: $3,2,3$. Then, we take the shared prime and multiply it with all of the other prime factors. $3\times2\times3\times3\times2=108$.
The following equation gives us an easy way to find the LCM:
where GCF is the greatest common factor.
It is also of interest to find the LCM of two or more monomials in the same way as the LCM of two or more numbers. For example, the LCM of monomials $12xy$ and $15x^2y$ is $60x^2y$, or mathematically written $[12xy,15x^2y]=60x^2y.$ In general, the LCM can be a number, a variable or a combination of numbers and variables.
The LCM work with steps shows the complete step-by-step calculation for finding the least common multiple of a given set of integers: $5, 20, 40, 80, 100$ using the prime factorization. For any other set of numbers, just supply the list of numbers and click on the "GENERATE WORK" button. The grade school students may use this LCM calculator to generate the work, verify the results of adding, subtracting, or comparing fractions, derived by hand or do their homework problems efficiently.
Real World Problems Using LCM
In problems of adding, subtracting, or comparing fractions, we usually use the least common multiple. The least common denominator of two or more fractions is the LCM of the denominators. Similarly, the least common denominator for algebraic fractions is the LCM of their denominators. For instance, if we compare two or more fractions, one way is to write them using the LCD. Then we need to rewrite our fractions as new equivalent fractions, etc.
LCM Practice Problems
Practice Problem 1:
Find the LCM of $72$ and $128$
Practice Problem 2:
In the store, red pencils come in packages of $14$, while blue pencils come in packages of $17$.
If we want to purchase the same number of red and blue pencils, find the smallest number of red pencils that we must buy.
The LCM calculator, formula, step by step calculation, real world problems and practice problems would be very useful for grade school students (K-12 education) to learn how to find the least common multiple of two or more numbers. It is helpful in many situations in mathematics, particularly in adding, subtracting, or comparing fractions.

