Pythagorean Theorem Calculator

Q: What is Pythagoras theorem?

If c is the length of the hypotenuse and a and b are the lengths of the legs in a right triangle, then the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs, i.e. c^2 = a^2 + b^2

Length of side `a`

Length of side `b`

Length of side `c` = 5

GENERATE WORK

Pythagorean Theorem - work with steps

Input Data :
`a` = 3
`b` = 4

Objective :
Find the unknown length `c` of right triangle.

Formula :
`c = \sqrt(a^2 + b^2)`

Solution :
`c = \sqrt(3^2 + 4^2)`
` = \sqrt(9 + 16)^`
` = \sqrt(25)`
`c = 5`

Pythagorean Theorem calculator calculates the length of the third side of a right triangle based on the lengths of the other two sides using the Pythagorean theorem. In other words, it determines:

The length of the hypotenuse of a right triangle, if the lengths of the two legs are given;
The length of the unknown leg, if the lengths of the leg and hypotenuse are given.

The hypotenuse of a right triangle is always the side opposite to the right angle. It is the longest side in a right triangle. The other two sides are called the legs of a right triangle. In a right triangle $\Delta ABC$ where the right angle is at vertex $C$, the length of sides are usually denoted by $a,b$ and $c$ and the measures of acute angles are denoted by $\alpha=m\angle A$ and $\beta=m\angle B$. Therefore, the leg $a$ is across from the angle $\angle A$, the leg $b$ is across from the angle $\angle B$ and the hypothenuse $c$ is across from the right angle $\angle C$.

Pythagorean theorem formula to find unknown side of a triangle

Pythagorean theorem calculator is an online Geometry tool requires lengths of two sides of a right triangle $\Delta ABC$

It is necessary to follow the next steps:

Enter the lengths of two sides of a right triangle in the box. These values must be positive real numbers or parameters. Note that the length of a segment is always positive;
Press the "GENERATE WORK" button to make the computation;
Pythagorean theorem calculator will give the length of the third side of a right triangle.

Input: Two positive real numbers or parameters as two side lengths of a right triangle $\Delta ABC$.
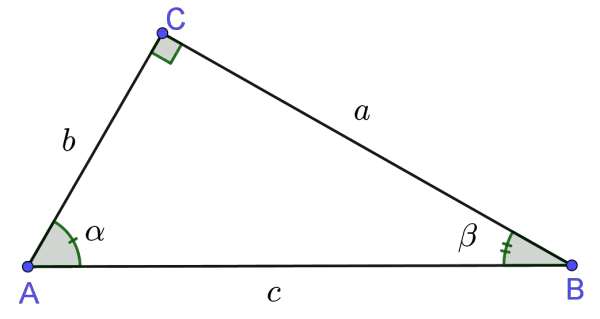
Output: A positive real number or variable as the length of the third side a right triangle $\Delta ABC$

Pythagorean Theorem Formula:

In a right triangle $\Delta ABC$, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs, i.e. $$c^2=a^2+b^2,$$ where $c$ is the length of the hypotenuse and $a$ and $b$ are the lengths of the legs of $\Delta ABC$.
We must make sure that the length of the hypotenuse is labeled by $c$ and the lengths of the legs are labeled by $a$ and $b$.
If we know the length of the hypotenuse and the length of one leg, then the length of the other leg can be calculated by the formula $$a^2=c^2-b^2$$ or $$b^2=c^2-a^2$$

What is Pythagoras theorem?

One of the most famous and most useful theorems in mathematics is the Pythagoras Theorem. The theorem is named after the Greek mathematician Pythagoras because he gave its first proof, although no evidence of it exists.

Pythagorean Theorem: If $c$ is the length of the hypotenuse and $a$ and $b$ are the lengths of the legs in a right triangle, then the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs, i.e. $$c^2=a^2+b^2$$
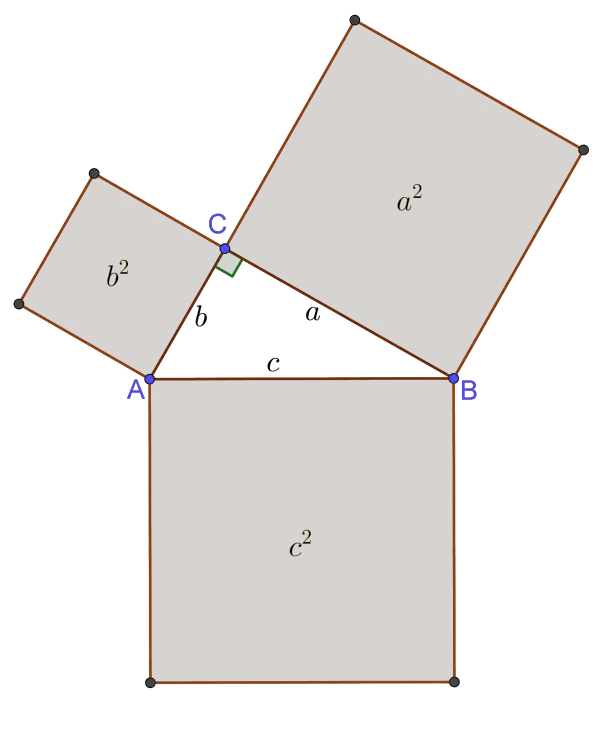
Thus, if we know the lengths of two out of three sides in a right triangle, we can find the length of the third side. The Pythagorean Theorem can also be expressed in terms of area. In a right triangle, the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the two legs.

Pythagorean Theorem expressed in terms of area

There are many proofs of the the Pythagorean Theorem. For example, an idea of proof is given by considering the pictures below (Rufus Isaac, Two Mathematical Papers without Words, Mathematics Magazine, Vol. 48 (1975), p. 198). Let us consider two congruent squares. The area of big square (blue) on the first picture is equal to the sum of the areas of two small squares (both in blue) on the second picture.

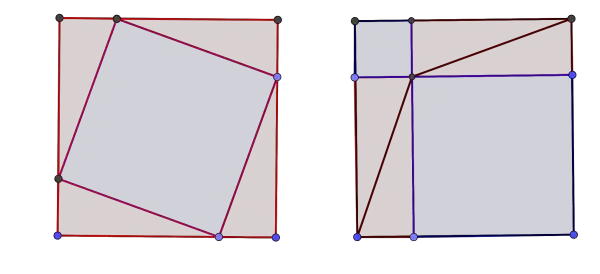
The converse of the Pythagoras Theorem is also valid. The Pythagorean converse theorem can help us in classifying triangles.

If the square of the length of the longest side of a triangle is equal to the sum of squares of the lengths of the other two sides, then the triangle is a right triangle.
If the square of the length of the longest side of a triangle is less than the sum of the squares of the lengths of the other two sides, then the triangle is an acute triangle.
If the square of the length of the longest side of a triangle is greater than the sum of the squares of the lengths of the other two sides, then the triangle is an obtuse triangle.

How to Find a Unknown Side of a Right Triangle?

In a right triangle $\Delta ABC$, the length of the hypotenuse $c$ is equal to the square root of the sum of the squares of the lengths of the legs $a$ and $b$. That means,

$$c=\sqrt{a^2+b^2}$$

In a right triangle $\Delta ABC$, the length of either leg is equal to the square root of the difference of the squares of the length of the hypotenuse and the length of the other leg. That means,

$$a=\sqrt{c^2-b^2}\quad{\rm or}\quad b=\sqrt{c^2-a^2}$$

Pythagorean Theorem calculator work with steps shows the complete step-by-step calculation for finding the length of the hypothenuse $c$ in a right triangle $\Delta ABC$ having the lengths of two legs $a=3$ and $b=4$. For any other combinations of side lengths, just supply lengths of two sides and click on the "GENERATE WORK" button. The grade school students may use this Pythagoras theorem calculator to generate the work, verify the results or do their homework problems efficiently.

Real World Problems Using Pythagorean theorem

The Pythagoras Theorem is widely applied in mathematics. The formula for finding distance between two points is based on the Pythagorean Theorem. For any two points $A(x_A,y_A)$ and $B(x_B,y_B)$ in the two-dimensional Cartesian coordinate plane, the formula for distance between these points is derived from the Pythagorean Theorem, i.e.

$${AB}^2=(x_B-x_A)^2+(y_B-y_A)^2$$

Similarly, it is cited in the formula for distance between two points in the three-dimensional Cartesian coordinate space. The Pythagorean Theorem is also useful in finding the area of some polygon.
In the theory of numbers, a triple $(a, b, c)$ consisted of three positive integers $a, b,$ and $c,$ which satisfies the Pythagorean formula

$$a^2 + b^2 = c^2$$

is the Pythagorean Triple. If $(a, b, c)$ is a Pythagorean Triple, then so is $(ka, kb, kc$) for any positive integer $k$. For example, the Pythagorean Triples are: $(3, 4, 5),$ $(5, 12, 13),$ $(8, 15, 17),$ $(7, 24, 25),$ $(20, 21, 29),$ etc.
In the theory of complex numbers, the modulus $|z|$ of the complex number $z=a+ib$ is determined by

$$|z|=\sqrt{a^2+b^2}$$

These three magnitudes are related by the Pythagorean formula,

$$z^2=a^2+b^2$$

It means, the distance of the point $z$ from the origin $O(0,0)$ is $|z|$ in the complex plane.The distance between two complex numbers $z_1=a+ib$ and $z_2=c+id$ in the complex plane is also connected with the Pythagoras Theorem. Therefore, the distance between two complex numbers is

$$|z_1-z_2|=\sqrt{(a-c)^2+(b-d)^2}$$

In the trigonometry, for any acute angle $\angle A\; (m\angle A=\alpha)$ of a right triangle $\Delta ABC$, the Pythagorean Identify is valid

$$\sin^2\alpha+\cos^2\alpha=1$$

Pythagorean Theorem Practice Problems

Practice Problem 1:
A sail on a sailboat is in the shape of a right triangle. The length of the longest side of the sail is $220$ centimeters, and the length of the other side of the sail is $5$ meters.

Practice Problem 2:
Given a triangle $\Delta ABC$, as it is shown in the picture below. The altitude $\overline{AA'}$ divides the sides $\overline{BC}$ into two segments ${BA'}=5$ and ${CA'}=9$. Find the perimeter of the triangle $\Delta ABC$.

practice problem for pythagorean theorem

The Pythagorean Theorem calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) in classifying triangles, especially in studying right triangles. Their main purpose is to find the length of the third side of a right triangle when we know the lengths of the other two sides and apply this result in mathematical and real life situations.

Who invented Pythagorean Theorem?
Pythagorean theorem was invented by the Greek mathematician Pythagoras because he gave its first proof, although no evidence of it exists.

How do you calculate unknown or missing side of right triangle?
The length of unknown third side of right triangle can be found by using Pythagoras theorem. a = √(c^2 - b^2) is the formula to find the length a:, b = √(c^2 - a^2) is the formula to find the length b: and c = √(a^2 + b^2) is the formula to find the length c:.

What are the rules of Pythagoras?
The square of the length of the longest side of a triangle should be equal to the sum of squares of the lengths of the other two sides.

How do you solve a and b in Pythagorean theorem?
To find a: using Pythagorean theorem,

find the square value of side b.
find the square value of side c.
Subtract b^2 from c^2.
Find the root square value of the difference is the value of a.

To find b: using Pythagorean theorem,

find the square value of side c.
find the square value of side a.
Subtract c^2 from a^2.
Find the root square value of the difference is the value of b.

What is the hypotenuse calculator?
The tool which is used to find the long side of the right triangle is the hypotenuse calculator. Pythagorean theorem calculator is also known as hypotenuse calculator.

How do you make a^2+b^2 = c^2?
The equation a^2+b^2 = c^2 should be simplified further to find the unknown length of c. To simplify the equation, take the square root on both sides. The equation becomes √(a^2 + b^2) = c. Apply the values and find c:.

What is derived from the Pythagorean Theorem?
Pythagorean Theorem derives that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs in a right triangle ΔABC.

When would you use Pythagorean theorem in real life?
In real life situations, we can use Pythagorean theorem to find the length of a ladder to reach top of the building from the place where you are standing nearby (for example, you are standing 25 yards away from the building).