Mixed Numbers Multiplication Calculator

Mixed numbers multiplication calculator uses two mixed numbers, i.e. two numbers in terms of a whole numbers and proper fractions, $A\frac{a}{b}$ and $B\frac{c}{d}$ for positive integers $a,b,c$ and $d$, and multiples them. It is an online tool to find the product in the simplest form of two mixed numbers and give the stepwise procedure for multiplying two mixed numbers.
It is necessary to follow the next steps:

1. Enter two mixed numbers $A\frac{a}{b}$ and $B\frac{c}{d}$ in the box. These numbers must be in terms of whole numbers and proper fractions. The numerators and denominators in the proper fractions must be positive integers.
2. Press the "GENERATE WORK" button to make the computation;
3. Mixed numbers multiplication calculator will give the product of two numbers represented as mixed numbers.

Input : Two mixed numbers;
Output : A fraction in the simplest form or decimal number.

Conversion of Mixed Number to Improper Fraction Rule: The mixed number $A\frac{a}{b}$ for $a,b>0$ can be rewritten as improper fraction by the following formula $$A\frac{a}{b}=\frac{A\times b+a}{b},\quad \mbox{for}\;a,b>0$$ Mixed Numbers Multiplication Rule: The product of two mixed numbers $A\frac{a}{b}$ and $B\frac{c}{d}$ is determined by the following formula $$A\frac{a}{b}\times B\frac{c}{d}=\Big(\frac{A\times b+a}{b}\Big)\times\Big(\frac{B\times d+c}{d}\Big)=\frac{(A\times b+a)\times(B\times d+c)}{b\times d},\quad \mbox{for}\;a,b,c,d>0$$ Conversion of Improper Fraction to Mixed Number Rule: The improper fraction $\frac{a}{b}, a>b$ can be rewritten as mixed number by the following formula $$\frac{a}{b}=\Big[\frac a b\Big]\frac{a-\Big[\frac a b\Big]\times b}{b},\quad \mbox{for}\;b\ne0$$ where square brackets $[\; ]$ mean round down to the nearest integer.

How to Find the Product of Two Mixed Numbers?

A mixed number $A\frac ab$ or sometimes called a \underline{mixed fraction} represents the sum of a nonzero integer number $A$ and a proper fraction $\frac ab$. The numerator $a$ and denominator $b$ of the proper fraction must be positive integers. In the notation of mixed numbers, the sum does not explicitly use operator plus. For example, two pizza and one-third of another pizza is denoted by $2\frac 13$ instead of $2+\frac 13$. Negative mixed number, for example $-2\frac 13$ represents the sum $-(2+\frac 13)$. Mixed numbers can also be written as decimals, for example, $2\frac 12=2.5$.
Improper fractions are rational numbers where the numerator is greater than the denominator. Improper fractions can be rewritten as a mixed number in the following way:

• Divide the numerator by the denominator;
• The whole part of the quotient is the whole number of the mixed number;
• The reminder is the new numerator of the proper fraction;
• The denominator of the proper fraction is equal to the denominator of the improper fraction.

More precisely, the improper fraction $\frac{a}{b}, a>b,$ can be rewritten as a mixed number in the following way $$\frac{a}{b}=\Big[\frac a b\Big]\frac{a-\Big[\frac a b\Big]\times b}{b},\quad \mbox{for}\;b\ne0,$$ where square brackets $[\; ]$ mean round down to the nearest integer. For example, $\frac 8 5$ is equal to $1\frac 35$.
To rewrite a mixed number to an improper fraction follow the next steps:

• Multiply the denominator of the proper fraction by the whole number in the mixed number and add it to its numerator;
• The denominator of the improper fraction is equal to the denominator of the proper fraction of the mixed number.

This means, a mixed number $A\frac{a}{b}$ for $a,b>0$ can be rewritten as improper fraction in the following way $$A\frac{a}{b}=\frac{A\times b+a}{b},\quad \mbox{for}\;a,b>0$$ For example, $$10\frac 35=\frac{10\times5+3}{5}=\frac{53}5$$ Multiplication of mixed numbers or variables may be indicated by a multiplication sign $\times$ between two numbers, a dot between two numbers, or parentheses around one or both of numbers. For instance, $$2\frac{1}{3}\times 3\frac{1}{2},\quad 2\frac{1}{3}\cdot3\frac{1}{2},\quad\Big(2\frac{1}{3}\Big) 3\frac{1}{2}, \quad2\frac{1}{3}\Big( 3\frac{1}{2}\Big),\quad \Big(2\frac{1}{3}\Big) \Big(3\frac{1}{2}\Big)$$ To multiply mixed numbers, convert them to improper fractions then multiply the fractions. The product of two mixed numbers $A\frac{a}{b}$ and $B\frac{c}{d}$ can be expressed by the formula $$A\frac{a}{b}\times B\frac{c}{d}=\Big(\frac{A\times b+a}{b}\Big)\times\Big(\frac{B\times d+c}{d}\Big)=\frac{(A\times b+a)\times(B\times d+c)}{b\times d},\quad \mbox{for}\;a,b,c,d>0$$ For example, let us multiply fractions $7\frac{1}{6}$ and $2\frac{1}{3}$. After converting these numbers to improper fractions, we obtain $$7\frac{1}{6}=\frac {1\times 6+1}{6}=\frac {43}{6}\;\mbox{and}\;2\frac{1}{3}=\frac {2\times 3+1}{6}=\frac {7}{6}$$ Thus, the multiplication of two mixed numbers is equivalent to the multiplication of a fraction by another fraction. To recall, the multiplication of a fraction by another fraction is determined by the following steps:

1. Multiply the numerators;
2. Multiply the denominators;
3. Simplify the product if needed.

So,
$$7\frac{1}{6}\times 2\frac{1}{3}=\frac{43}{6}\times\frac{7}{6}=\frac{43\times7}{6\times6}=\frac{301}{18}$$ To write the product as a mixed number, we use the above mentioned conversion from an improper fraction to a mixed number: $$ \frac{301}{18}=16\frac{13}{18}$$ The Mixed Numbers Multiplication work with steps shows the complete step-by-step calculation for finding the product of two mixed numbers $7\frac{1}{6}$ and $2\frac{1}{3}$ using the mixed numbers multiplication rule. For any other mixed numbers, just supply two mixed numbers in terms of a whole number and proper fraction and click on the GENERATE WORK button. The grade school students may use this mixed numbers multiplication calculator to generate the work, verify the results of multiplying numbers derived by hand, or do their homework problems efficiently.

Real World Problems Using Mixed Numbers Multiplication

Mixed numbers are useful in counting whole things and parts of these things together. It is used primarily in measurement. Especially of interest are mixed numbers whose denominator of the fractional part is a power of two. They are commonly used with U.S. customary units such as inches, pounds, etc. For instance, $1\; {\rm inch}=2\frac{54}{100}\; \rm{cm}$.
We can use an area model to explain the multiplication of the mixed number. The area model is one strategy that can help us to find a product of small mixed numbers. For example, let us find the product $3\frac 12\times 2\frac 13 $. The problem can be graphically represented by the following picture:

This product can be rewritten as $$\Big(3+\frac 12\Big)\times \Big(2+\frac 13\Big)=3\times2+3\times \frac 13+\frac 12\times 2+\frac 12 \times \frac 13 $$ Area is measured in squares (or square units). The yellow rectangle has area of $6$ squares, the red rectangle has area of $1$ square, the blue rectangle has area of $1$ square and the purple rectangle has area of $\frac 1 6$ of the square unit. If we add these areas, the product of $4\frac 5 {12}$ and $3\frac {2} 9$ is $8\frac16$.

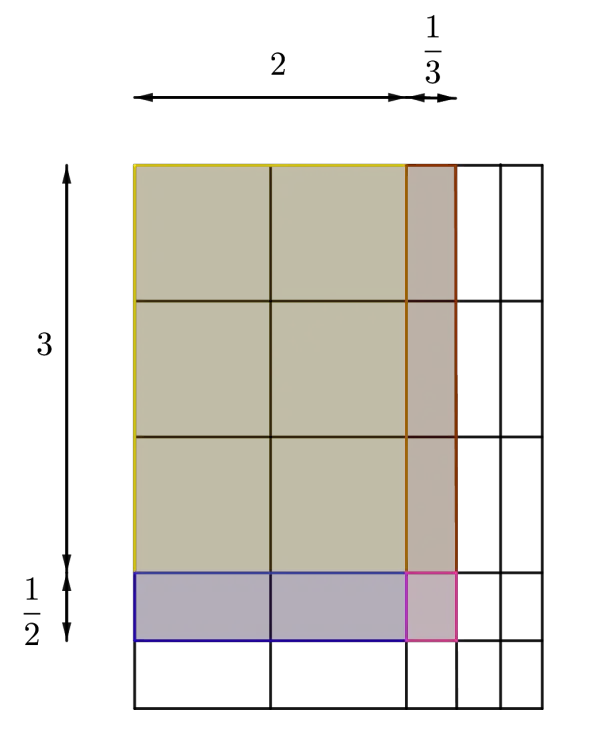
Mixed Numbers Multiplication Practice Problems

Practice Problem 1 :
Find the product of $4\frac 5 {12}$ and $3\frac {2} 9$ and write the result in the simplest form.

Practice Problem 2 :
Ann ate $1 \frac12$ pizza while Michael ate $2 \frac 13$ times as much than Ann, how many pizzas did Michael eat?

The mixed numbers multiplication calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the multiplication of two or more numbers represented as mixed numbers. Using this concept they can be able to solve complex algebraic problems and equations.