Slope Intercept Form Calculator

Slope intercept form calculator uses slope $m$ and $y$-intercept $b$ to find the equation of a line in the two-dimensional Cartesian coordinate plane. This calculator allows us to find the equation of a line in the general form $Ax+By+C=0$. It's an online Geometry tool requires the coefficient $m$ which represents how $y$ changes with each one unit of $x$ and the coefficient $b$ which represents where the line crosses $y$-axis.

It is necessary to follow the next steps:

1. Enter coefficients for the slope $m$ and the $y$-intercept $b$ in the box. These values must be real numbers or parameters;
2. Press the "GENERATE WORK" button to make the computation;
3. Slope intercept form calculator will give the equation of line in the general form. This line passes through the point with coordinates $(0,b)$ and has the slope $m$.

Input: Real numbers or variables as coefficients of the slope $m$ and the $y$-intercept $b$.
Output: An equation of a line in the general form, $Ax+By+C=0$.

Slope Intercept Form Formula:

What is the Slope Intercept Form?

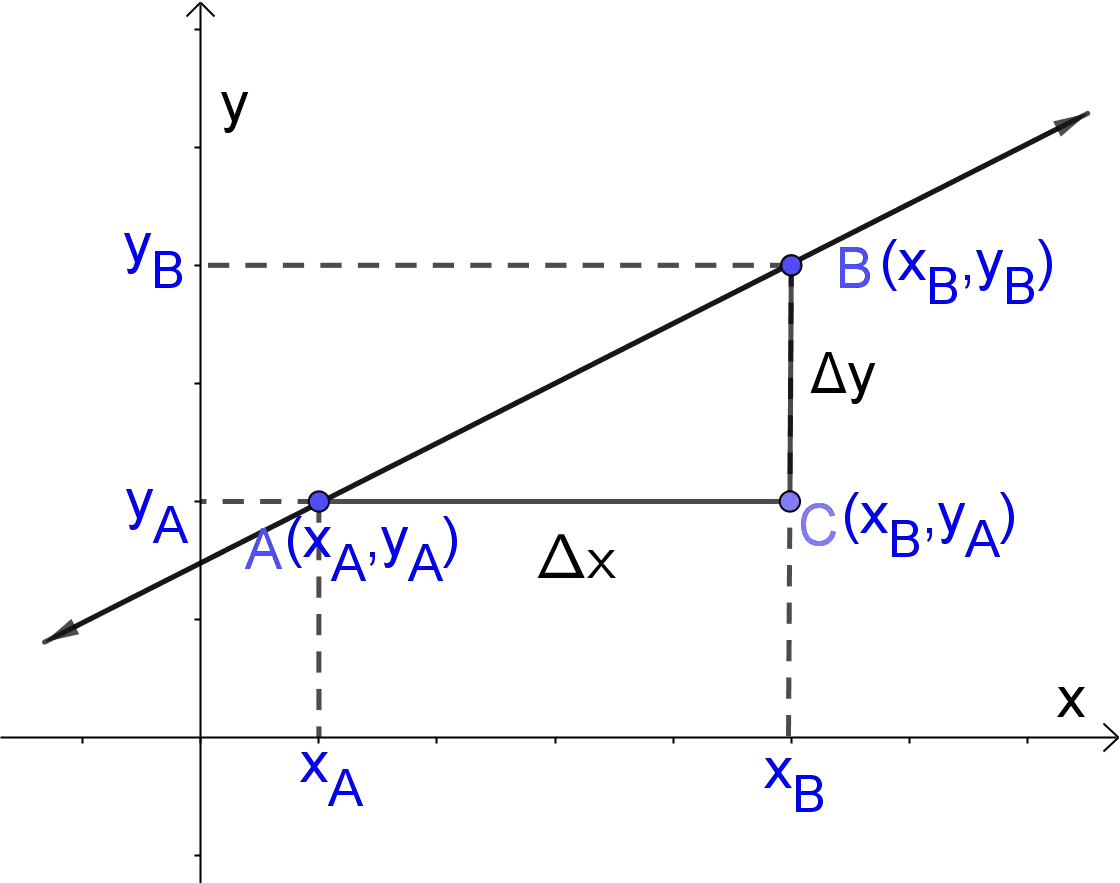
A line in the two-dimensional Cartesian coordinate plane can be described as a relationship between the vertical and horizontal positions of points which belong to the line. This relation can be written as $y =f(x)$. One of the form of the line in the two-dimensional Cartesian coordinate plane is the slope intercept form, $y = mx + b$, where $m$ and $b$ are real numbers. For example, the graphical representation of the line $y=8x+10$ is given in the picture below. So, the slope is $8$ and the $y$-intercept is $10$. This means that the line passes thought point $(0,10)$. The slope intercept work with steps shows the complete step-by-step solution for this example.

The slope of a line in the two-dimensional Cartesian coordinate plane is usually represented by the letter $m$, and it is sometimes called the rate of change between two points. This is because it is the change in the $y$-coordinates divided by the corresponding change in the $x$ -coordinates between two distinct points on the line. If we have coordinates of two points $A(x_A,y_A)$ and $B(x_B,y_B)$ in the two-dimensional Cartesian coordinate plane, then the slope $m$ of the line through $A(x_A,y_A)$ and $B(x_B,y_B)$ is fully determined by the following formula $$m=\frac{y_B-y_A}{x_B-x_A}$$ In other words, the formula for the slope can be written as $$m=\frac{\Delta y}{\Delta x}=\frac{{\rm vertical \; change}}{{\rm horizontal \; cnahge}}=\frac{{\rm rise}}{{\rm run}}$$ As we know, the Greek letter $\Delta$, means difference or change. The slope $m$ of a line $y=mx+b$ can be defined also as the rise divided by the run. Rise means how high or low we have to move to arrive from the point on the left to the point on the right, so we change the value of $y$. Therefore, the rise is the change in $y$, $\Delta y$. Run means how far left or right we have to move to arrive from the point on the left to the point on the right, so we change the value of $x$. The run is the change in $x$, $\Delta x$. The slope $m$ of a line $y=mx+b$ describes its steepness. For instance, a greater slope value indicates a steeper incline. There are four different types of slope:

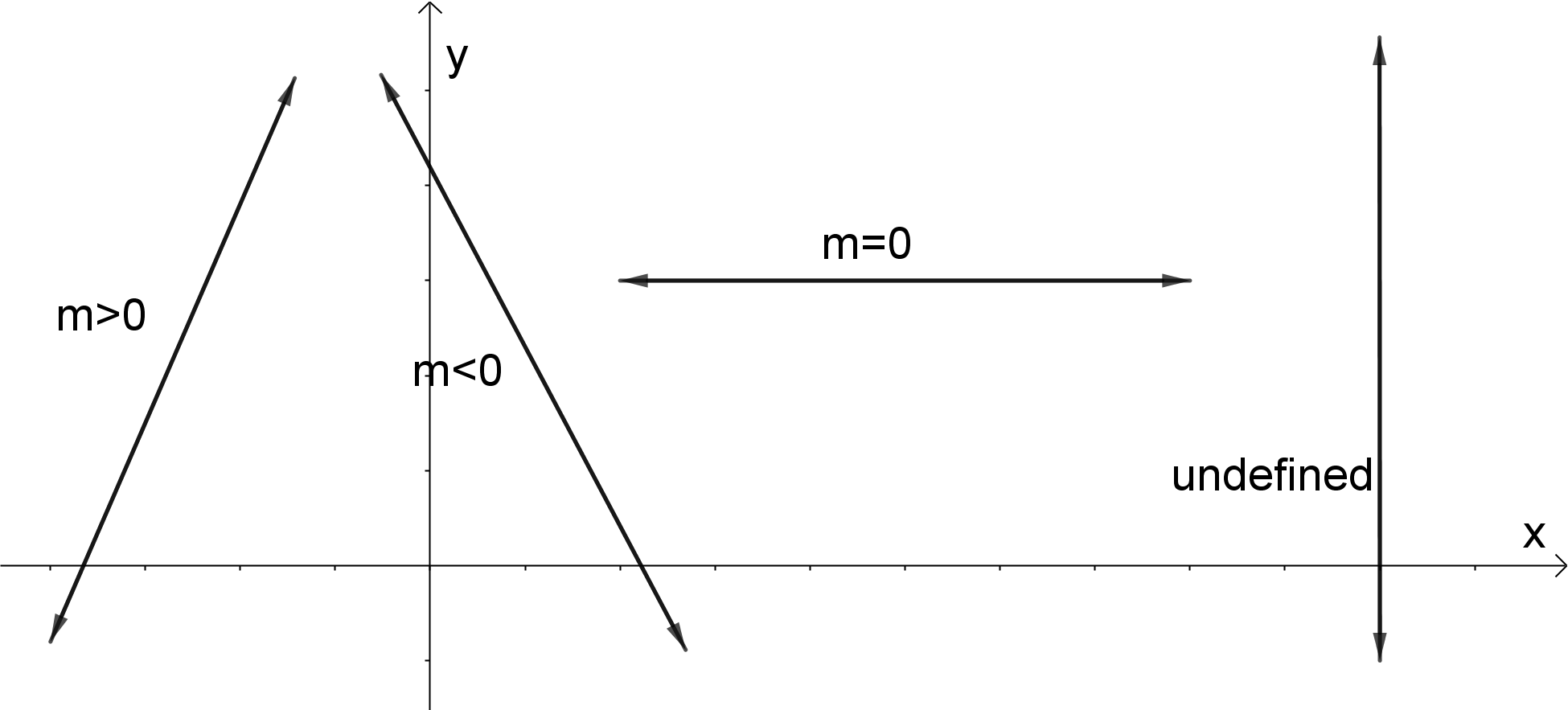
1. Positive slope $m>0$, if a line $y=mx+b$ is increasing, i.e. if it goes up from left to right;
2. Negative slope $m<0$, if a line $y=mx+b$ is decreasing, i.e. if it goes down from left to right;
3. Zero slope, $m=0$, if a line $y=mx+b$ is horizonal. In this case, the equation of the line is$y=b$;
4. Undefined slope, if a line $y=mx+b$ is vertical. This is because division by zero leads to infinities. So, the equation of the line is $x=a$.All vertical lines $x=a$ have an infinite or undefined slope.

The $y$-intercept of a line is the point $(0,b)$ at which the line crosses the $y$-axis. It is usually denoted by $b$. There are three ways to find the $y$-intercept:

• If we graphically represent the line;
• If we plug in the value $x=0$ in the equation of line and solve for $y$;
• If we put the linear equation into slope intercept form, and find $b$ in the equation of line.

How to Find Slope Intercept Form of Line?

From the general form of the line, $Ax+By+C=0,$ we obtain $$y=-\frac{A}{B}x-\frac{C}{B},\quad B\ne 0$$ Therefore, if $B\ne0$, then the slope is $m=-\frac{A}{B}$ and the $y$-intercept is $b=-\frac{C}{B}$.
If $B=0$, then the slope is undefined and the $y$-intercept does not exist, i.e. the equation of the line is $x=a$.
If we plug in the given values of the slope $m$ and the $y$-intercept $b$ into the equation $y=mx+b$, we will obtain the equation of the line that passes through the point $(0,b)$ and has the slope $m$. In many cases, we can find the equation of the line by hand, especially for integer values of $b$ and $m$. But, if the input values are big real number or number with many decimals, then we should use the line pass through point calculator to get an accurate result.
The slope intercept work with steps shows the complete step-by-step calculation for finding the general equation of the line with the slope $m=8$ and the $y$-intercept $b=10$. For any other combinations of slope and $y$-intercept, just supply coefficients of slope and $y$-intercept and click on the "GENERATE WORK" button. The grade school students may use this slope intercept form calculator to generate the work, verify the results or do their homework problems efficiently.

Real World Problems Using Slope and Slope Intercept Form

The fundamental applications of slope or the rate of change are in geometry, especially in analytic geometry. But, the rate of change is also fundamental to the study of calculus. For non-linear functions, the rate of change varies along the function. \underline{The first derivative} of the function at a point is the slope of the tangent line to the function at the point. So, the first derivative is the rate of change of the function at the point.
In physics, in definitions of some magnitudes such as displacement, velocity and acceleration, the rate of change play important role. For instance, the rate of change of a function is connected to the average velocity.
The rate of change can be found also in many fields of life, for instance population growth, birth and death rates, etc.
Linear models in science and real life can be described in the slope intercept form.
In physics, if a object moves with constant acceleration, the velocity, $v$, is given by the equation $$v = at + v_0$$ where $a$ is the constant acceleration, $v_0$ is the initial velocity and $t$ is the time. This equation is well known as a kinematic equation. We can conclude that this equation has the slope intercept form.
In statistics, we can calculate a regression line for two variables. A regression line is a line that best fits the data. The formula for the regression line is $y = mx + b$, where $m$ is the slope of the line and $b$ is the $y$-intercept.

Slope Intercept Practice Problems

Practice Problem 1 :
Michael has $\$300$ in his bank account. He gets a job, $\$8$ per hour, and he deposits all earnings in his account. Write the equation for this problem in slope intercept form.

Practice Problem 2 :
The slope of line is $-12$ and the line crosses the $y$-axis at the point $(0,-2)$. Find the slope intercept form of the line.

The slope intercept form calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students of K-12 education to learn what are different equations of a line in geometry, how to find the general equation of a line. They will be able to solve real-world problems using linear models in slope intercept form.