Area & Perimeter of a Square Calculator
Area and Perimeter of Square - work with steps
Input Data :
length = 8 in
Objective :
Find what the is area of square?
Solution :
Area = side x side
= 8 x 8
Area = 64 in²
Area & Perimeter of a Square calculator uses side length of a square, and calculates the perimeter, area and diagonal length of the square. It is an online Geometry tool requires side length of a square. Using this calculator, we will understand the algorithm of how to find the the perimeter, area and diagonal length of a square.
It is necessary to follow the next steps:
- Enter the side length of a square in the box. The value must be positive real numbers or parameter. Note that the length of a segment is always positive;
- Press the "GENERATE WORK" button to make the computation;
- Square calculator will give the area, perimeter and diagonal length of a square.
OUput : Three positive real numbers or variables as the perimeter, area and diagonal length of a square and corresponding units after that.
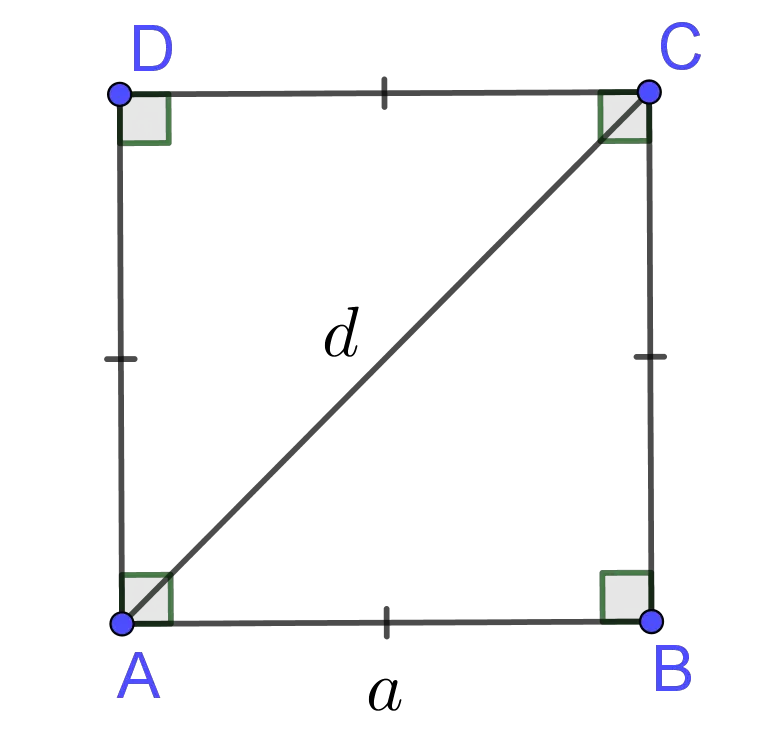
The perimeter of a square is determined by the following formula
$$P=4\times a$$ where $a$ is the length of the side of square.
Area of Square Formula::
The area of a square is determined by the following formula
$$A=a\times a=a^2$$ where $a$ is the length of the side of square.
Area of Square (Diagonal) Formula:
The area of a square is determined by the following formula $$A=\frac{d\times d}2=\frac {d^2}2$$ where $d$ is the length of the diagonal of square.
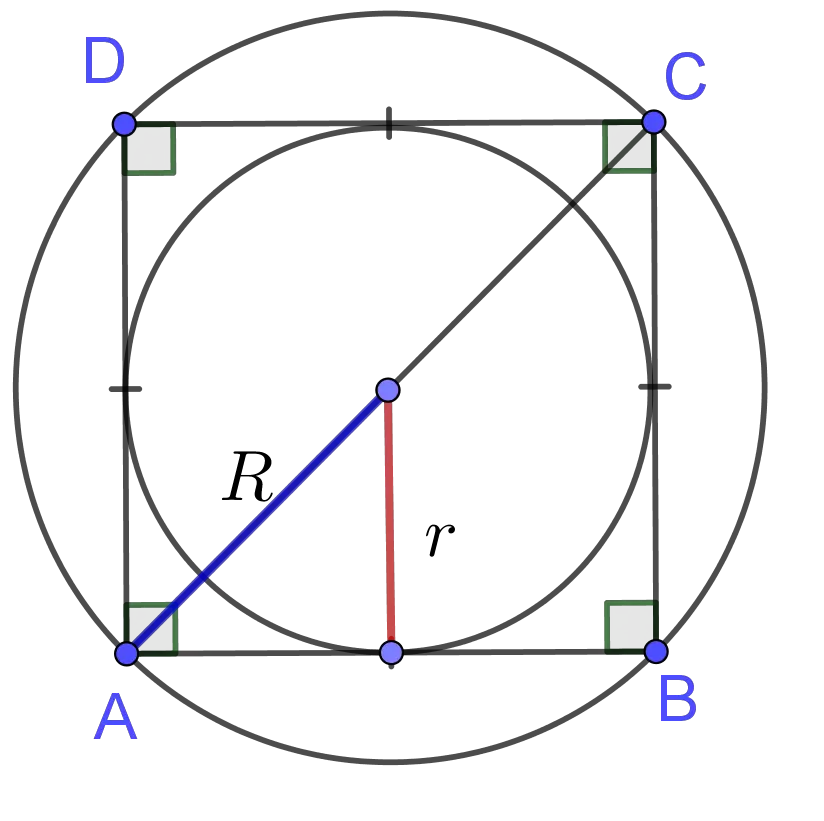
Area of Square (Circumradius) Formula:
The area of a square is determined by the following formula $$A = 2 R^2$$ where $R$ is the length of the circumradius of square.
Area of Square (Inradius) Formula:
The area of a square is determined by the following formula $$A = 4 r ^2 $$ where $r$ is the length of the inradius of square.
What is Area & Perimeter of Square?
A quadrilateral with four congruent angles and four congruent sides is \underline{a square} (see the picture below).
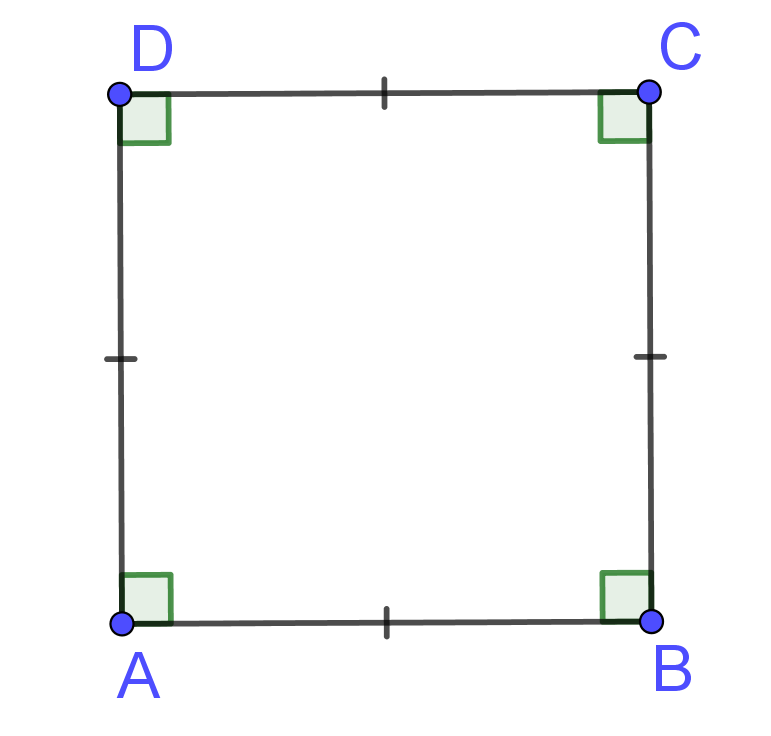
A square is a rectangle but every rectangle is not a square because a square has four congruent sides, whereas a rectangle does not have. Therefore, all the properties of rectangles can be applied to squares. So, a square is both a rhombus and a rectangle.
The following characteristics describe a square:
- Diagonals bisect the opposite angles of the square;
- Diagonals are perpendicular and bisect each other;
- Diagonals are congruent;
The distance around a square is called the perimeter of the square. It is usually denoted by $P$. To find the perimeter of square we add the lengths of its sides. Thus, the perimeter of a square with side length of $a$ is

- In function of the circumradius $R$: $$A = 2 R^2$$
- In function of inradius $r$: $$A = 4 r ^2 $$

The area and perimeter of a square work with steps shows the complete step-by-step calculation for finding the perimeter, area and diagonal length of the square with side length of $8\; in$ using the perimeter, area and diagonal length formulas. For any other length of side, just supply positive real number and click on the GENERATE WORK button. The grade school students may use this area and perimeter of a square to generate the work, verify the results of perimeter and area of two dimensional figures derived by hand or do their homework problems efficiently.
Real World Problems Using Area & Perimeter of a Square
We usually solve problems regarding perimeters and areas of two-dimensional shapes. For example, to find the total area and perimeter of square garden or, to paint the walls of the room. In order to buy the corresponding amount of paint, we need to know the area of walls. Calculating area of a floor is important to determine the number of tiles needed or the size of a carpet to be fitted. Squares are very useful in architecture, construction, plumbing, engineering, landscaping, etc. Many people such architects, engineers, and many others need to calculate areas and perimeters of squares as part of their daily job.
Square Practice Problems
Practice Problem 1:
A square playground has an area of $140 m^2$. Find the length of the side of the playground?
Practice Problem 2:
A square basketball court is $15$ meters long. Find the perimeter of the court?
The square calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the concept of area and perimeter of square. This concept can be of significance in geometry, to find the perimeter and area of complex figures, as well as in real life for everyday needments.

