Linear Interpolation Calculator

Linear interpolation calculator uses coordinates of two points $A(x_A, y_A)$ and $B(x_B, y_B)$ and $x$-coordinate of the interpolated point $C$ in the two-dimensional Cartesian coordinate plane and find the $y$-coordinate of the interpolated point $C$. It's an online Geometry tool requires coordinates of 2 points and $x$-coordinate of the interpolated point in the two-dimensional Cartesian coordinate plane.

It is necessary to follow the next steps:

1. Enter coordinates $(x_A, y_A), (x_B, y_B)$ of two points $A$ and $B$ and $x$-coordinate of the interpolated point $C$ in the box. These values must be real numbers or parameters;
2. Press the "GENERATE WORK" button to make the computation;
3. Linear interpolation calculator will give the $y$-coordinate of the interpolated point $C$. This point belongs to the line through points $A$ and $B$.

Input: Two ordered pairs of real numbers or variables and one real number or variable. Note that first coordinates in ordered pairs must be different.
Output: A real number or variable.

Linear Interpolant Formula:
$y$-Coordinate of Interpolated Point:$y$-coordinate of the point $C$ on the linear interpolant $AB$ is determined by the following equation $$\begin{align} y_C&=\frac{y_B(x_C-x_A)+y_A(x_B-x_C)}{x_B-x_A}\end{align}$$ where $x_C$ is the point coordinate of $C$, $(x_A,y_A)$ and $(x_B,y_B)$ are point coordinates of $A$ and $B$, respectively.

What is Linear Interpolation?

Information, especially numerical, appears in all areas of life and science. We can find the equation of a line of best fit, well known as regression line, and use it to minimize the distance of points which represent collection of data to the regression line. The regression line is a good method if the relation between the dependent and the independent variables is linear.
There are some other methods, such as the linear interpolation and the linear extrapolation. Interpolation is the method of finding a point between two points on a line or curve. More precisely,

• If we want to find coordinates of a point between two given points, then we use the linear interpolation
• If we want to find coordinates of a point that is not between two given points, then we use the linear extrapolation.

In other words, the linear interpolation is used to fill the gaps in a collection of points. The procedure for linear interpolation is to find a line that passes through the given points then to find the coordinates of a point between the given points. For example, given two points $A(x_A,y_A)$ and $B(x_B,y_B)$, as it is shown in the picture below. Firstly, we will find the line that contains the points $A$ and $B$. For a value $x$ in the interval $(x_1,x_2)$, the value $y$ along the non-vertical line through $A$ and $B$ is determined from the slopes $$\frac{y-y_A}{x-x_A}=\frac{y_B-y_A}{x_B-x_A}$$ Solving the previous equation for $y$, we obtian $$\begin{align} y&=\frac{y_B-y_A}{x_B-x_A}(x-x_A)+y_A\\ &=\frac{y_B(x-x_A)+y_A(x_B-x)}{x_B-x_A} \end{align}$$ This line is called thelinear interpolant between these points. Since the point $C$ belongs to this line, it's coordinates $(x,y)$ can be found by linear interpolation. For non-linear collection of data, linear interpolation is often not accurate. If the points in the collection of data change by a large amount in the interval, then we use a curve instead of a line to estimate values between points. This method is well-known as polynomial interpolation.

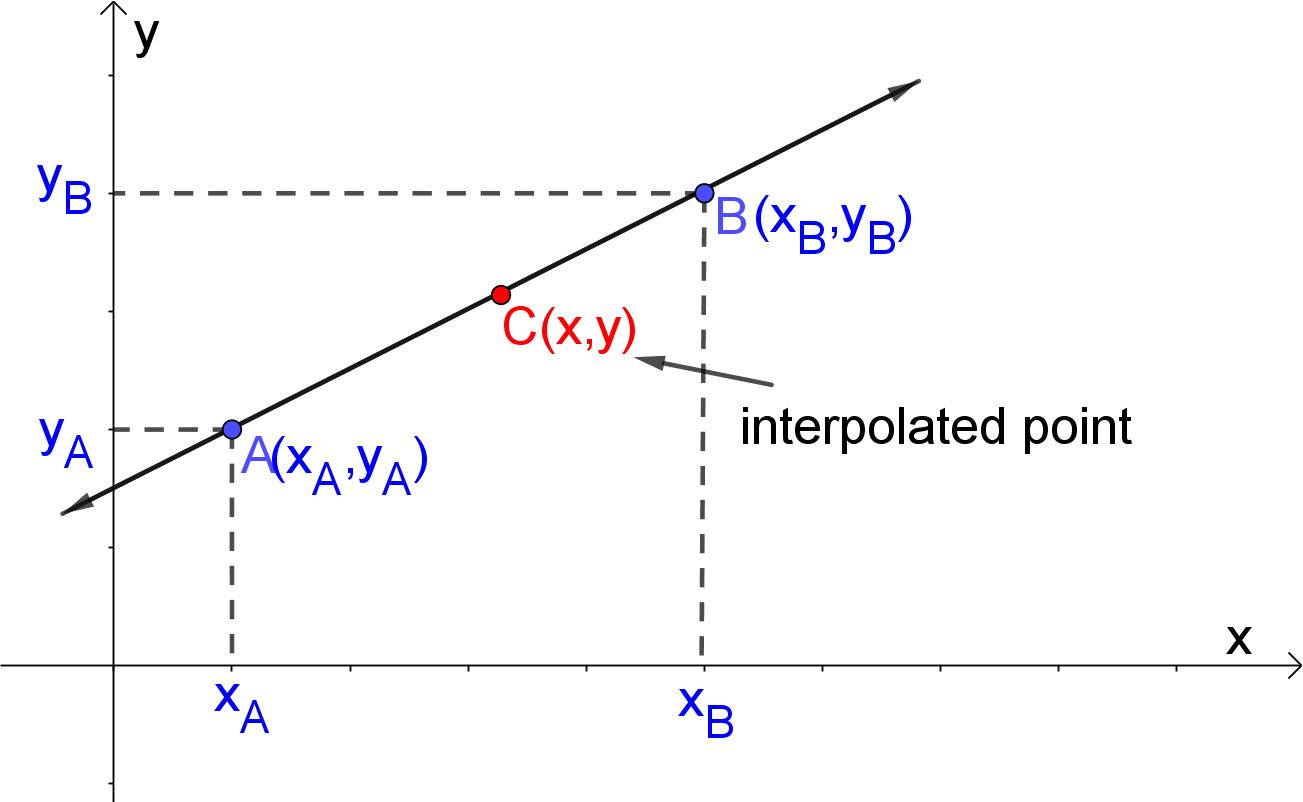
How to Find Linear Interpolation of Line?

If we plug in the coordinates of the points $A$ and $B$, $(x_A,y_A)$ and $(x_B,y_B)$, into the equation $$y=\frac{y_B-y_A}{x_B-x_A}(x-x_A)+y_A $$ we get the equation of the linear interpolant. By substituting the coordinate $x_C$ of the point $C$ in the equation of the linear interpolant, we will obtain the missing coordinate of the point $C$. Therefore, the missing $y$-coordinate of the point $C$ is determined by the following equation $$\begin{align} y_C&=\frac{y_B-y_A}{x_B-x_A}(x_C-x_A)+y_A\\ &=\frac{y_B(x_C-x_A)+y_A(x_B-x_C)}{x_B-x_A}\end{align}$$ The Linear interpolation work with steps shows the complete step-by-step calculation for finding the value of the $y$-coordinate of an interpolated point, with the value of the x-coordinate of $3$, on the line through points with coordinates $(2, 4)$ and $(7, 8)$. For any other combination of coordinates, just supply the coordinates of 2 points and the first coordinate of the required interpolated point and click on the "Generate Work" button. The grade school students may use this Linear Interpolation Calculator to generate the work, verify the results or do their homework problems efficiently.

Applications or Use of Linear Interpolation

Interpolation estimates the value of a function between two known values. The linear interpolation equation can be implemented in some mathematical package, for example in Microsoft Excel or MATLAB, provided the tabulated values are monotonic in $x$ and there is no equal $x$ values. So, if we need to predict values between two existing data points, then we use the linear interpolation method.
The linear interpolation is commonly used in computer graphics. For instance, Bresenham's algorithm interpolates points incrementally between the two endpoints of a line (Bresenham, J.E., Algorithm for computer control of a digital plotter, IBM Systems Journal, Vol 4, No 1, (1965), pp 2530.) The bilinear interpolation is a generalization of linear interpolation for interpolating functions of two variables $f(x,y)$. Firstly, we perform a linear interpolation in one direction, and then in the other direction.

Linear Interpolation Practice Problems

Practice Problem 1 : According to the statistics from $2011$ and $2015$, $20$ percent and $35$ percent of world population smokes, respectively. Using the linear interpolation estimate the percentage of smokers in $2012$.

Practice Problem 2 : Find the value of $y$ at $x=6$, if the two points are given $(1, 4)$ and $(5, 8).$

The Linear interpolation calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to learn how to find interpolated point coordinates on a line segment. This method is very useful in mathematics and real-world problems to predict values between two given data points.