Area and Circumference of Circle Calculator
Area, Circumference & Diameter of Circle - work with steps
Input Data :
Radius = 8 in
Objective :
Find the area of circle.
Solution :
Area = πr2
= 3.14 x (8)2
= 3.14 x (64)
Area = 201.1429 in²
Area and circumference of circle calculator uses radius length of a circle, and calculates the perimeter and area of the circle.
It is an online Geometry tool requires radius length of a circle. Using this calculator, we will understand methods of how to find the perimeter and area of a circle.
It is necessary to follow the next steps:
- Enter the radius length of a circle in the box. The value must be positive real number or parameter. Note that the length of a segment is always positive;
- Press the "GENERATE WORK" button to make the computation;
- Circle calculator will give the perimeter and area of a circle.
Output : Two positive real numbers or variables as the perimeter and area of a circle and corresponding units after that.
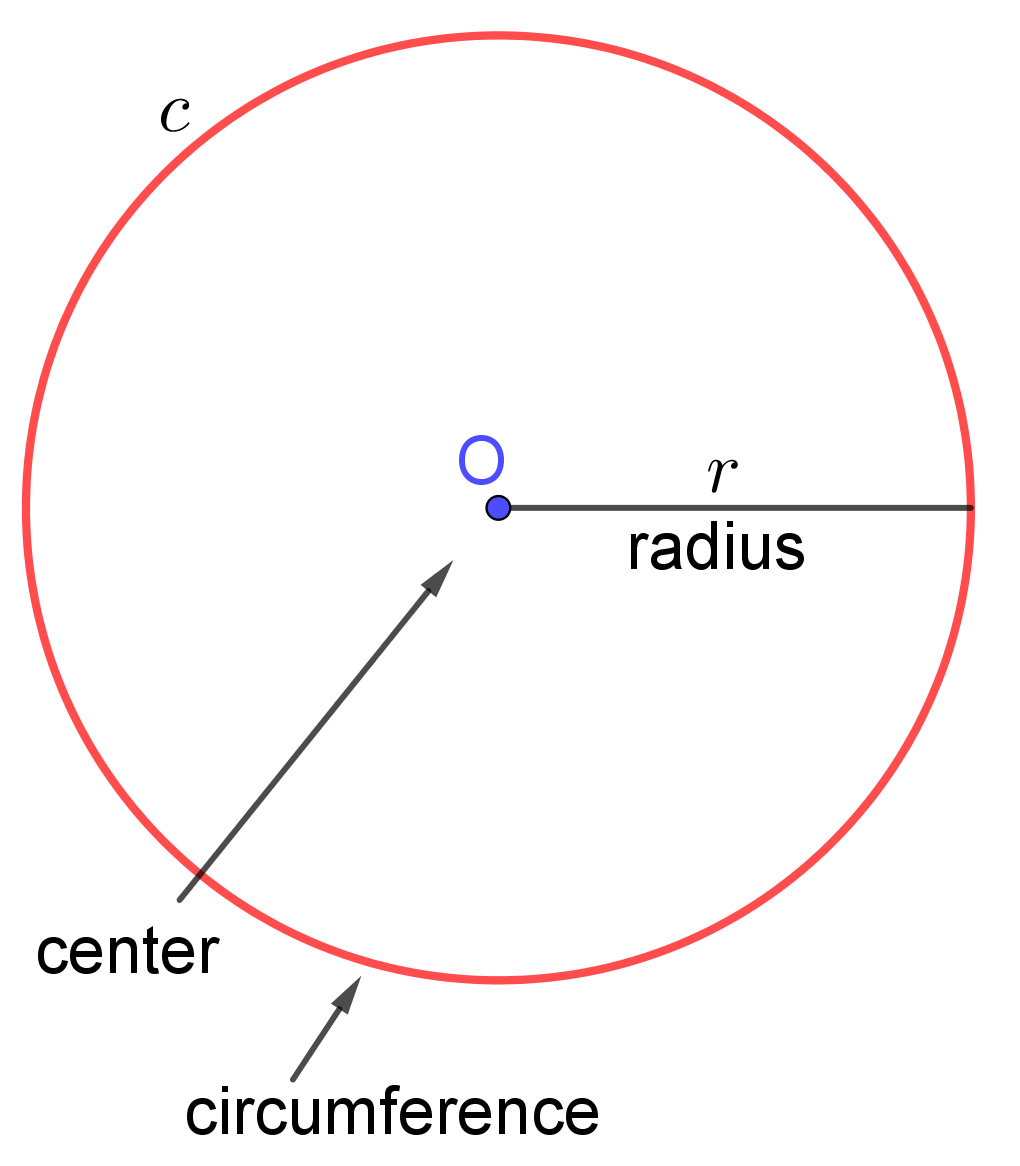
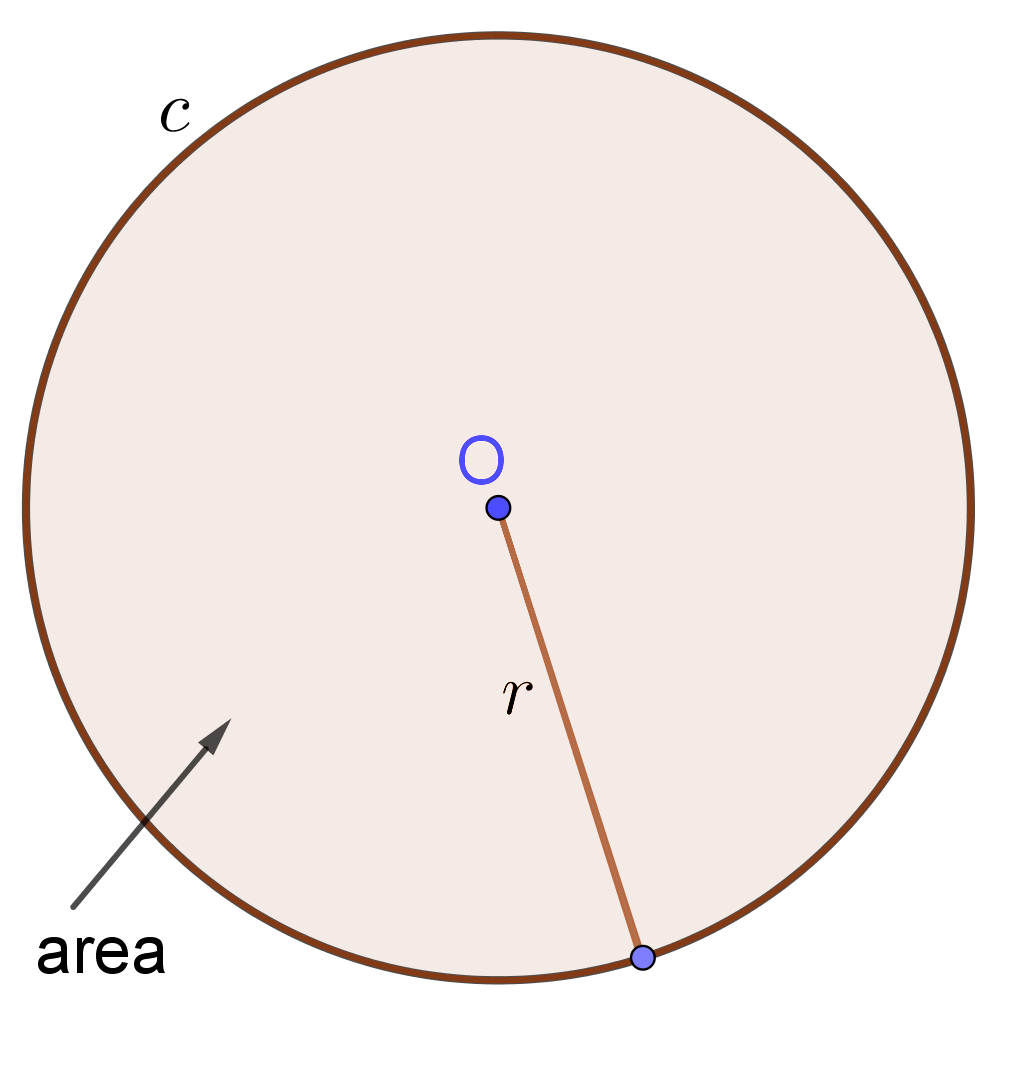
Circumference (Perimeter) of Circle Formula: The circumference of a circle is determined by the following formula $$C=2\times r\times\pi$$ where $r$ is the length of the radius of the circle and $\pi\approx3.14$.
Area of Circle Formula: The area of a circle is determined by the following formula $$A=r\times r\times\pi=r^2\times \pi$$ where $r$ is the length of the radius of the circle and $\pi\approx3.14$.
What is Area & Perimeter of Circle?
A set of points in a plane equally distanced from a given point $O$ is a circle. The point $O$ is called the center of the circle.
The distance from the center of a circle to any point on the circle is called the radius of this circle.A radius of a circle must be a positive real number. The circle with a center $O$ and a radius $r$ is denoted by $c(O,r)$.
The distance around a circle is called the perimeter or circumference of the circle. It is usually denoted by $C$.

If all vertices of a polygon belong on a circle, then the polygon is called inscribed. If all sides of a polygon are tangent to a circle, then the polygon is called circumscribed.
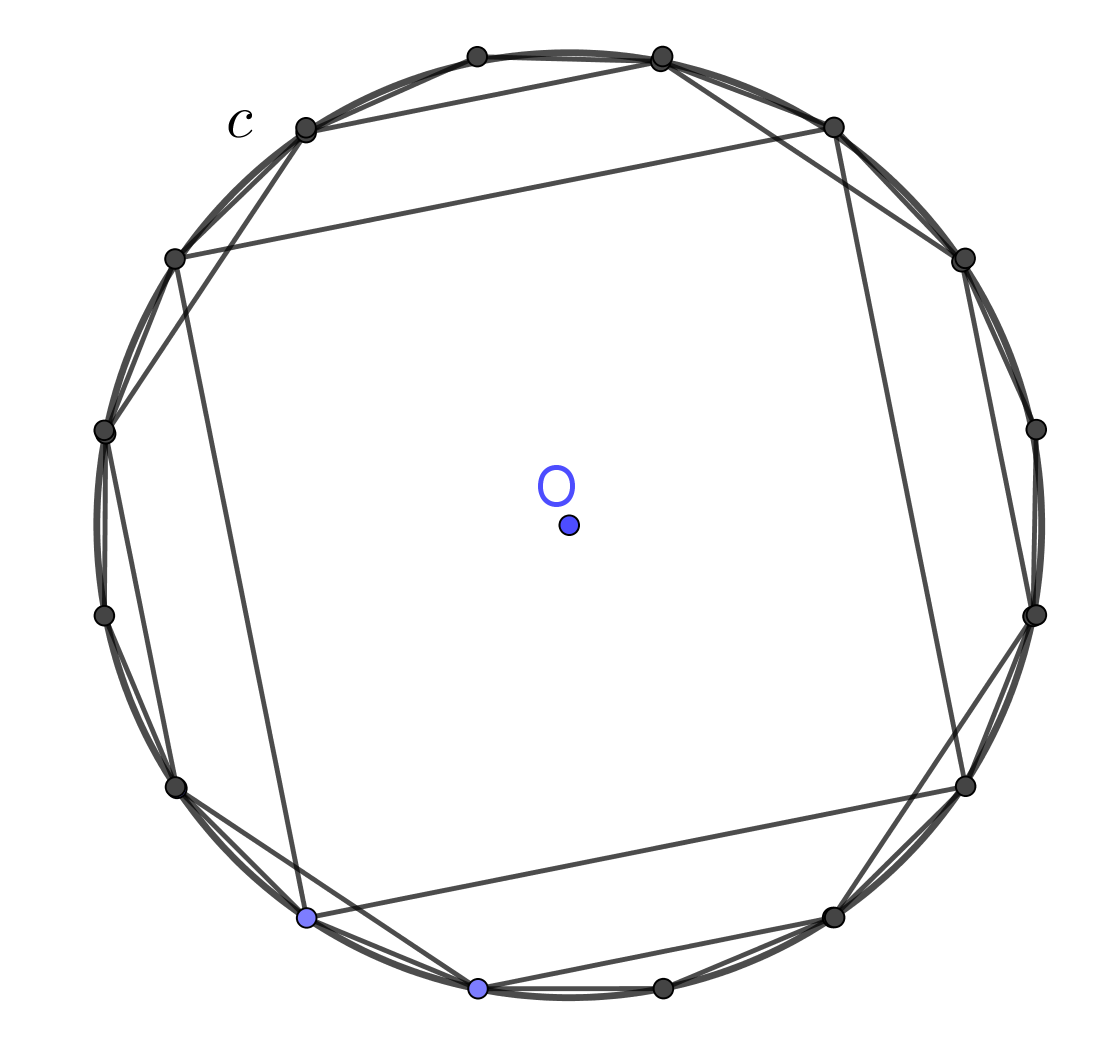
Method for finding circumference of circle: Let us inscribe into a circle a regular polygon, for example square. Then double the number of sides of this polygon to get octagon. If we continue the process of doubling the number of sides of regular inscribed polygons, we obtain an infinite sequence of perimeters of regular polygons which increases. This increasing sequence is bounded, since perimeters of all inscribed convex polygons are less than the perimeter of any circumscribed polygon. So, this increasing sequence of perimeters has a certain limit. This limit is the circumference. Hence, the circumference of a circle is the limit of the perimeter of a regular polygon inscribed into the circle when the number of its vertices is doubled indefinitely. Because all circles are similar, the ratio of the circumference to the diameter is the same number for all circles. This ratio of circumference to diameter is denoted by the Greek letter $\pi\approx 3.14$. Thus, the formula for circumference is
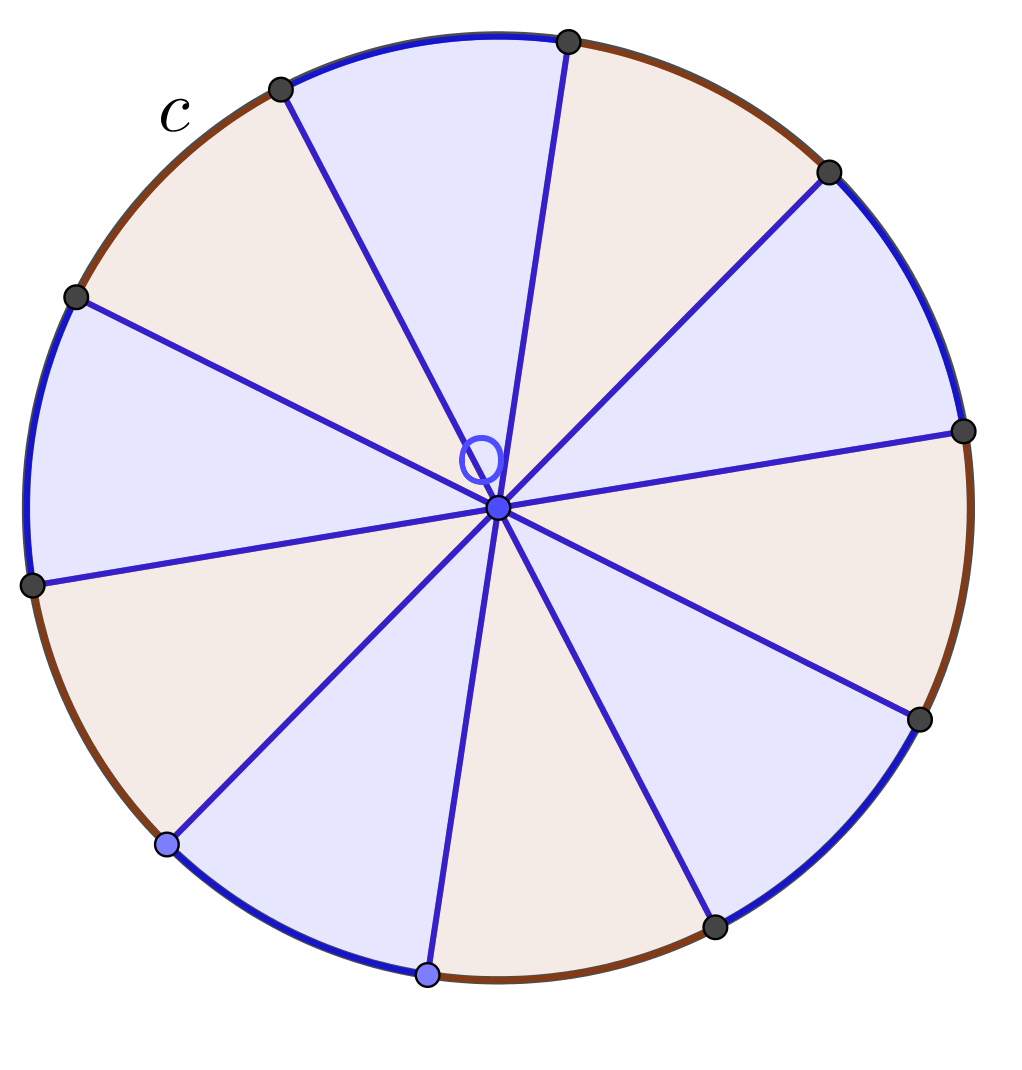
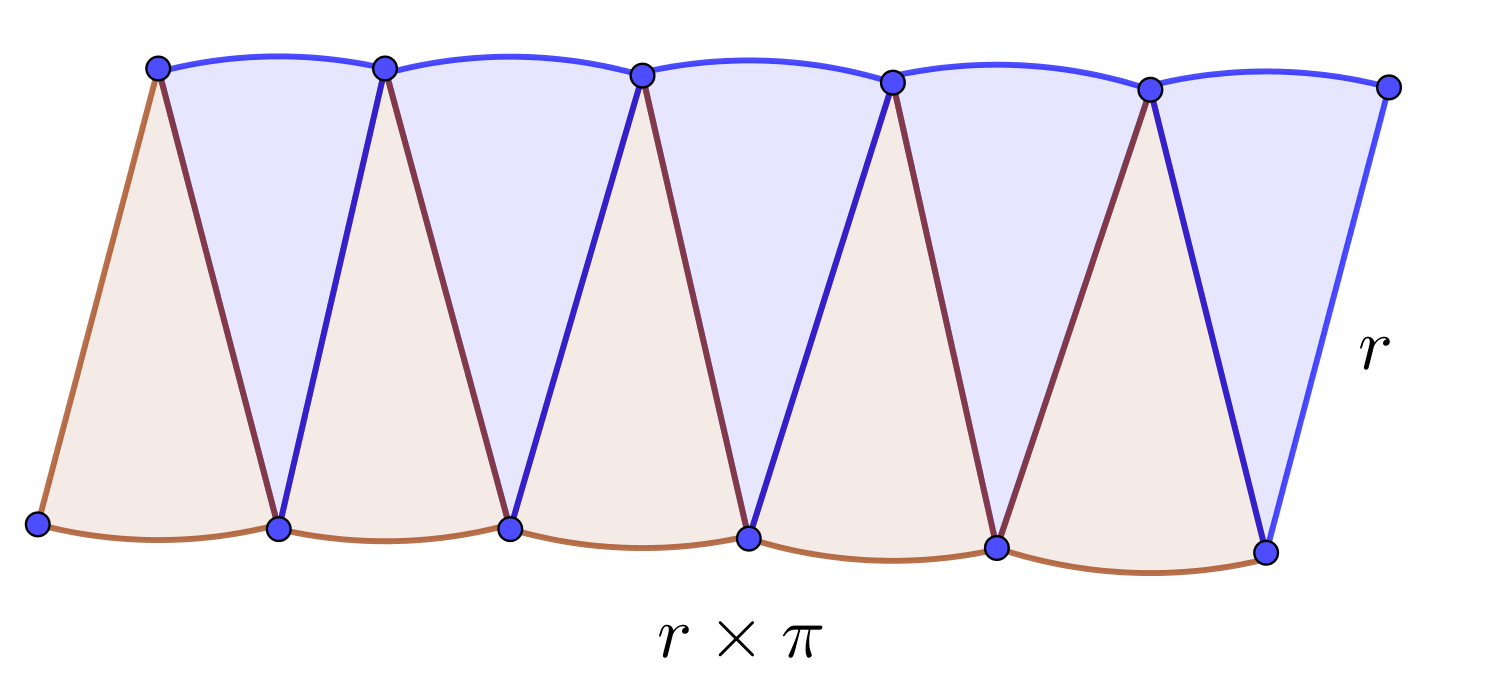
Method for finding area of circle: The area of a circle is the number of square units inside that circle. By dividing a circle into equal parts as shown in the picture below, we can rearrange the parts into an approximate rectangle. The length of this approximate rectangle equals the half of the circumference of the circle, $r\times\pi$. The width of this approximate rectangle is the radius $r$ of the circle. Since the area of a rectangle is the product of its length and width, the area of this approximate rectangle is
The Area and perimeter of a circle work with steps shows the complete step-by-step calculation for finding the circumference and area of the circle with the radius length of $8\;in$ using the circumference and area formulas. For any other value for the length of the radius of a circle, just supply a positive real number and click on the GENERATE WORK button. The grade school students may use this circle calculator to generate the work, verify the results of perimeter and area of two dimensional figures or do their homework problems efficiently. They can use these methods in order to determine the area and lengths of parts of a circle.
Real World Problems Using Area and Perimeter of a Circle
Calculating areas and circumferences of circles plays an important role in almost all field of science and real life. For instance, formula for circumference and area of a circle can be applied into geometry. They are used to explore many other formulas and mathematical equations. An arch length is a portion of the circumference of a circle.
The ratio of the length of an arc to the circumference is equal to the ratio of the measure of the arc to $360$ degrees. A sector of a circles is the region bounded by two radii of the circle and their intercepted arc.

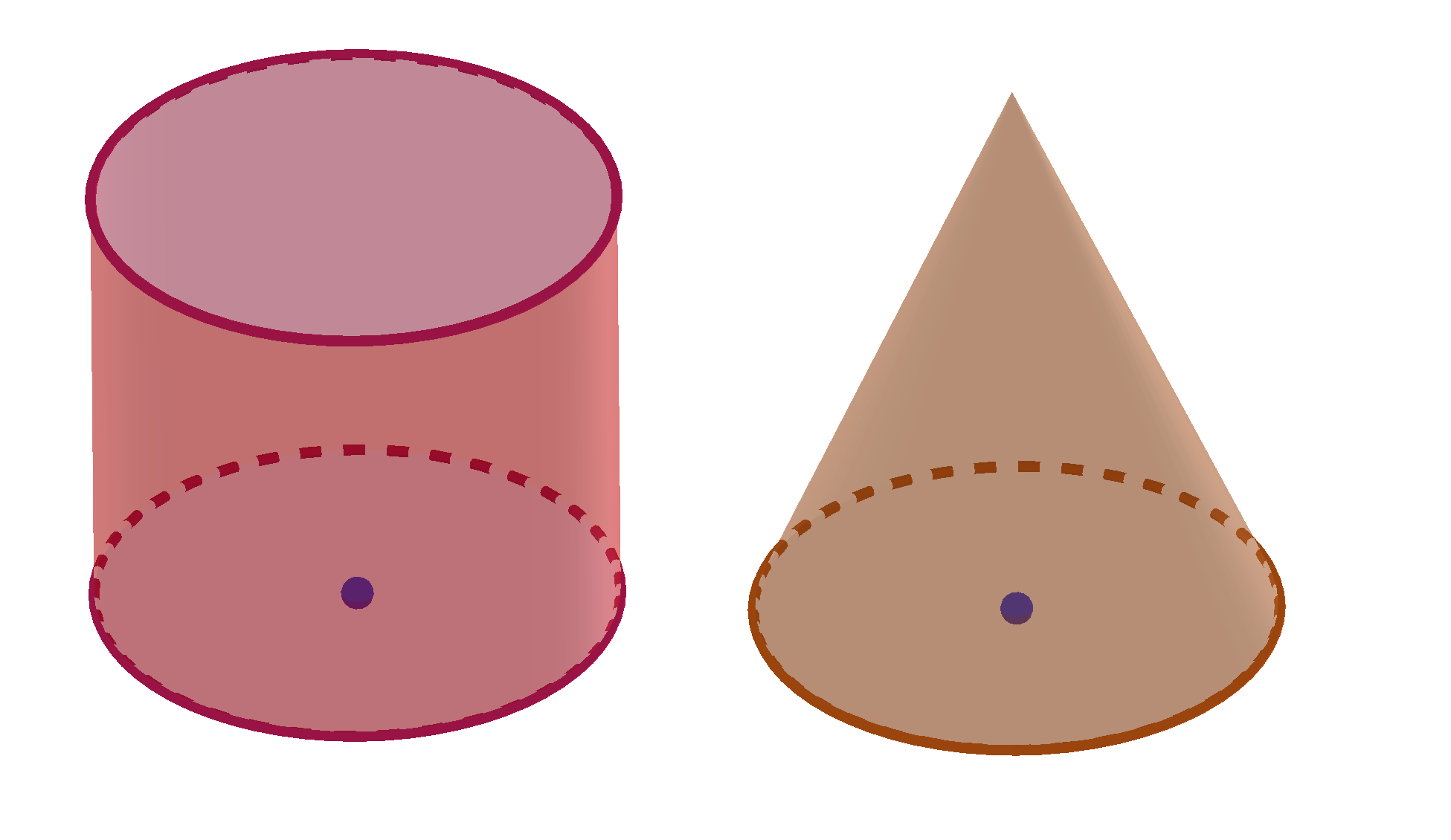
The surface area and volume of a cylinder and cone with circular bases contain the formula for area of circle. The lateral surface of a cone consists of all segments that connect the vertex with points on the base. If we cut it along the slant height then the lateral surface is the sector of a circle. So, the lateral area of a cone also uses the formula for area of circle.
Circle Practice Problems
Practice Problem 1:
A pizza is divided into $8$ equal pieces. The diameter of the pizza is $25$ centimeters. Find the area of one piece of pizza.
Practice Problem 2:
Given a tire with diameter of $100$ centimeters. How many revolutions does tire make while traveling $10$ kilometers?
The circle calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the concept of perimeter and area of circle. This concept can be of significance in geometry, to find the perimeter, area and volume of solids. Real life problems on circles involving arc length, sector of a circle, area and circumference are very common, so this concept can be of great importance of solving problems.

