Area & Perimeter of a Rectangle Calculator

Area & Perimeter of a Rectangle calculator uses length and width of a rectangle, and calculates the perimeter, area and diagonal length of the rectangle. It is an online Geometry tool requires two length sides of a rectangle. Using this calculator, we will understand the algorithm of how to find the perimeter, area and diagonal length of a rectangle.
It is necessary to follow the next steps:

1. Enter the length and width of a rectangle in the box. These values must be positive real numbers or parameter. Note that the length of a segment is always positive;
2. Press the "GENERATE WORK" button to make the computation;
3. Rectangle calculator will give the perimeter, area and diagonal length of a rectangle.

Input : Two positive real numbers or parameters as the length and width of a rectangle;
Output : Three positive real numbers or variables as the perimeter, area and diagonal length of a rectangle and corresponding units after that.
Rectangle Formula :

What is Area & Perimeter of Rectangle?

A quadrilateral with four congruent angles is a rectangle. The word "rectangle" comes from Latin "rectangulus". It's a combination of "rectus" which means "right" and "angulus" which means "an angle".
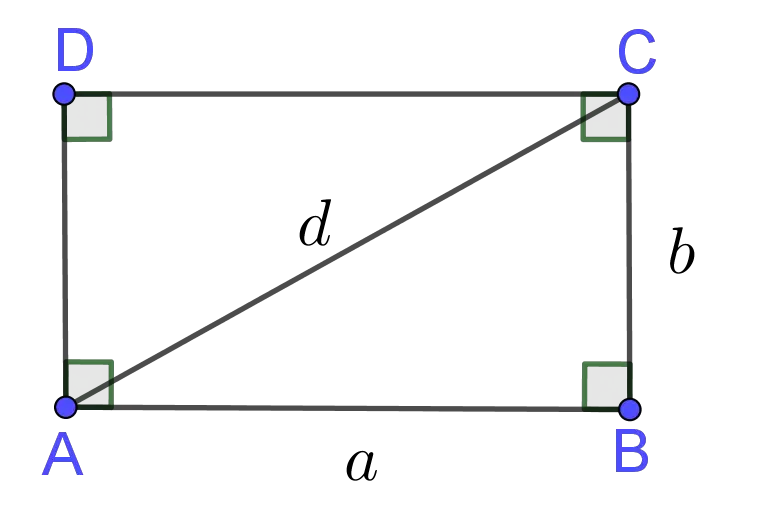
If $\angle A\cong\angle B\cong\angle C\cong\angle D$, then ${\overline{ABCD}}$ is a rectangle (see the picture below). It holds that

The lengths of its sides are denoted by $a$ and $b$, while the length of the diagonal is denoted with $d$. A rectangle is also called an equiangular quadrilateral, since all of its angles are congruent.
A rectangle is a parallelogram, but parallelogram is not a rectangle because in a rectangle each angle is a right angle, whereas it is not so in a parallelogram. That means that all the properties of a parallelogram can be also applied to rectangles. To recall, the parallelogram has the following properties:

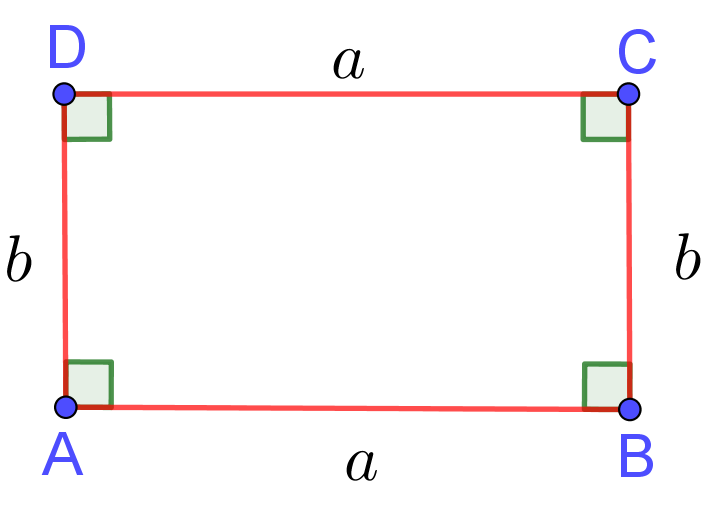
• Opposite sides of a parallelogram are congruent;
• Opposite angles of a parallelogram are congruent;
• The consecutive angles of a parallelogram are supplementary to each other;
• The diagonals of a parallelogram bisect each other

Rectangle satisfies one more property:

• The diagonals of a rectangle are congruent;

If we know side lengths of the rectangle, it is easy to calculate the length of the diagonal using the Pythagorean Theorem. A diagonal divides a rectangle into two right triangles. By applying the Pythagorean Theorem to $\Delta ABC$, we get
i.e. The rectangle has only two lines of symmetry. These lines are these ones which connect the midpoints of the opposite sides of the rectangle. A rectangle has central symmetry and rotational symmetry. The center of symmetry is the point of intersection of its diagonals, $O$.
The distance around a rectangle is called the perimeter of the rectangle. It is usually denoted by $P$. To find the perimeter of rectangle we add the lengths of its sides. Thus, the perimeter of a rectangle with the length of $a$ and the width of $b$ is
The area of a rectangle or some other polygon is a number of square units needed to fill the rectangle. The area, usually denoted by $A$, of a rectangle with the length of $a$ and the width of $b$ is In other words, the area of a rectangle is the product of its length and width.
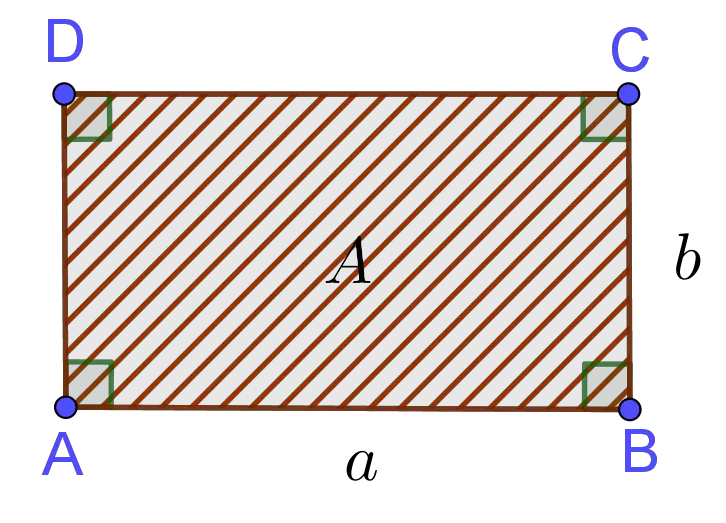
The perimeter is measured in units such as centimeters, meters, kilometers, inches, feet, yards, and miles. The area is measured in units units such as square centimeters $(cm^2)$, square meters $(m^2)$, square kilometers $(km^2)$ etc.

The area and perimeter of a rectangle work with steps shows the complete step-by-step calculation for finding the perimeter, area and diagonal length of the rectangle with the length of $5\;in$ and the width of $10 \;in$ using the perimeter, area and diagonal length formulas. For any other values for length and width of rectangle, just supply two positive real numbers and click on the GENERATE WORK button. The grade school students may use this area and perimeter of a rectangle to generate the work, verify the results of perimeter and area of two dimensional figures or do their homework problems efficiently.

Real World Problems Using Area & Perimeter of a Rectangle

Calculating areas and perimeters of various geometrical figures are very useful in real life problems. Rectangles often appear in real life. For instance, billboards, swimming pools, mobile phones, beds, doors, books. etc. If we need to make a deck along two sides of a swimming pool of rectangular shape, we must use the method for finding area of rectangle.
In three-dimensional geometry, some solids contains rectangular bases. For example, cube, rectangular prism, pyramid, etc. In problems of calculating surface area and volume of these solids we use formula for finding area of rectangle.

Rectangle Practice Problems

Practice Problem 1:
A rectangular garden is $2$ times long as its wide. If the perimeter of the garden is $48m$, find its area.

Practice Problem 2:
Find the length of the diagonal of a floor whose dimensions are $36\;in$ by $75\;in$.

The Area Perimeter of a Rectangle calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the concept of perimeter and area of rectangle. This concept can be of significance in geometry, to find the perimeter and area of complex figures, as well as to find surface area and volume of some solids. Real life problems on rectangles involving length, width, area, perimeter and diagonal are very common, so this can be of great the importance of solving.