Slope Calculator
Slope of Line - work with steps
Input Data :
Point A `(x_A, y_A)` = (3, 2)
Point B `(x_B, y_B)` = (7, 10)
Objective :
Find the slope of a line that passes through points A and B.
Formula :
`\text{Slope} m=\frac{y_B-y_A}{x_B-x_A}`
Solution:
`\text{Slope} m=\frac{10-2}{7-3}`
`=8/4`
m = 2
Slope calculator uses coordinates of two points $A(x_A,y_A)$ and $B(x_B,y_B)$ in the two-dimensional Cartesian coordinate plane and find the slope coefficient of a line that passes through $A$ and $B$. It's an online Geometry tool requires two point in the two-dimensional Cartesian coordinate plane and determines the slope or gradient of the line these points.
It is necessary to follow the next steps:
- Enter coordinates $(x_A,y_A)$ and $(x_B,y_B)$ of two points $A$ and $B$ in the box. These values must be real numbers or parameters;
- Press the "GENERATE WORK" button to make the computation;
- Slope calculator will give the slope of the line that passes through $A$ and $B$.
Output: A real number or parameter.
Slope Formula :
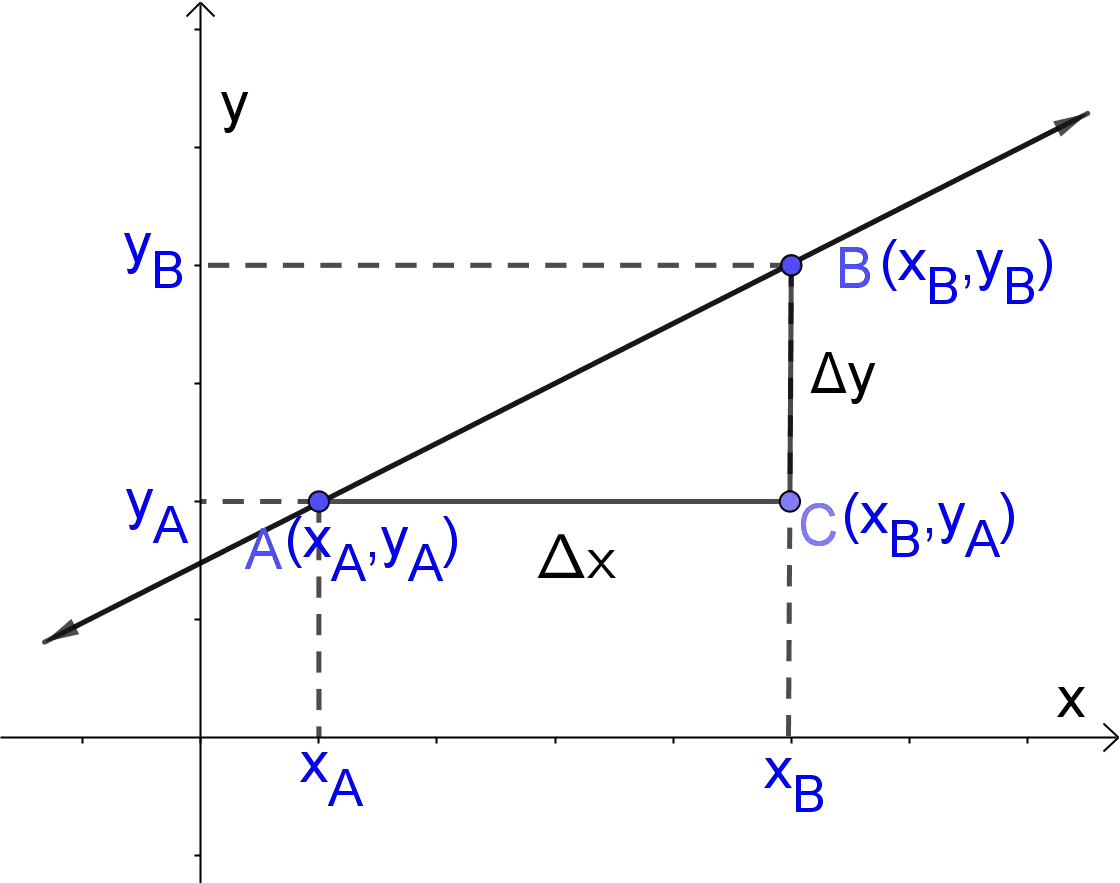
What is the Slope?
The slope of a line in the two-dimensional Cartesian coordinate plane is usually represented by the letter $m$, and it is sometimes called \underline{the rate of change} between two points. This is because it is the change in the $y$-coordinates divided by the corresponding change in the $x$ -coordinates between two distinct points on the line. If we have coordinates of two points $A(x_A,y_A)$ and $B(x_B,y_B)$ in the two-dimensional Cartesian coordinate plane, then the slope $m$ of the line through $A(x_A,y_A)$ and $B(x_B,y_B)$ is fully determined by the following formula $$m=\frac{y_B-y_A}{x_B-x_A}$$ In other words, the formula for the slope can be written as $$m=\frac{\Delta y}{\Delta x}=\frac{{\rm vertical \; change}}{{\rm horizontal \; change}}=\frac{{\rm rise}}{{\rm run}}$$ As we know, the Greek letter $\Delta$, means difference or change. The slope $m$ of a line $y=mx+b$ can be defined also as the rise divided by the run. Rise means how high or low we have to move to arrive from the point on the left to the point on the right, so we change the value of $y$. Therefore, the rise is the change in $y$, $\Delta y$. Run means how far left or right we have to move to arrive from the point on the left to the point on the right, so we change the value of $x$. The run is the change in $x$, $\Delta x$.

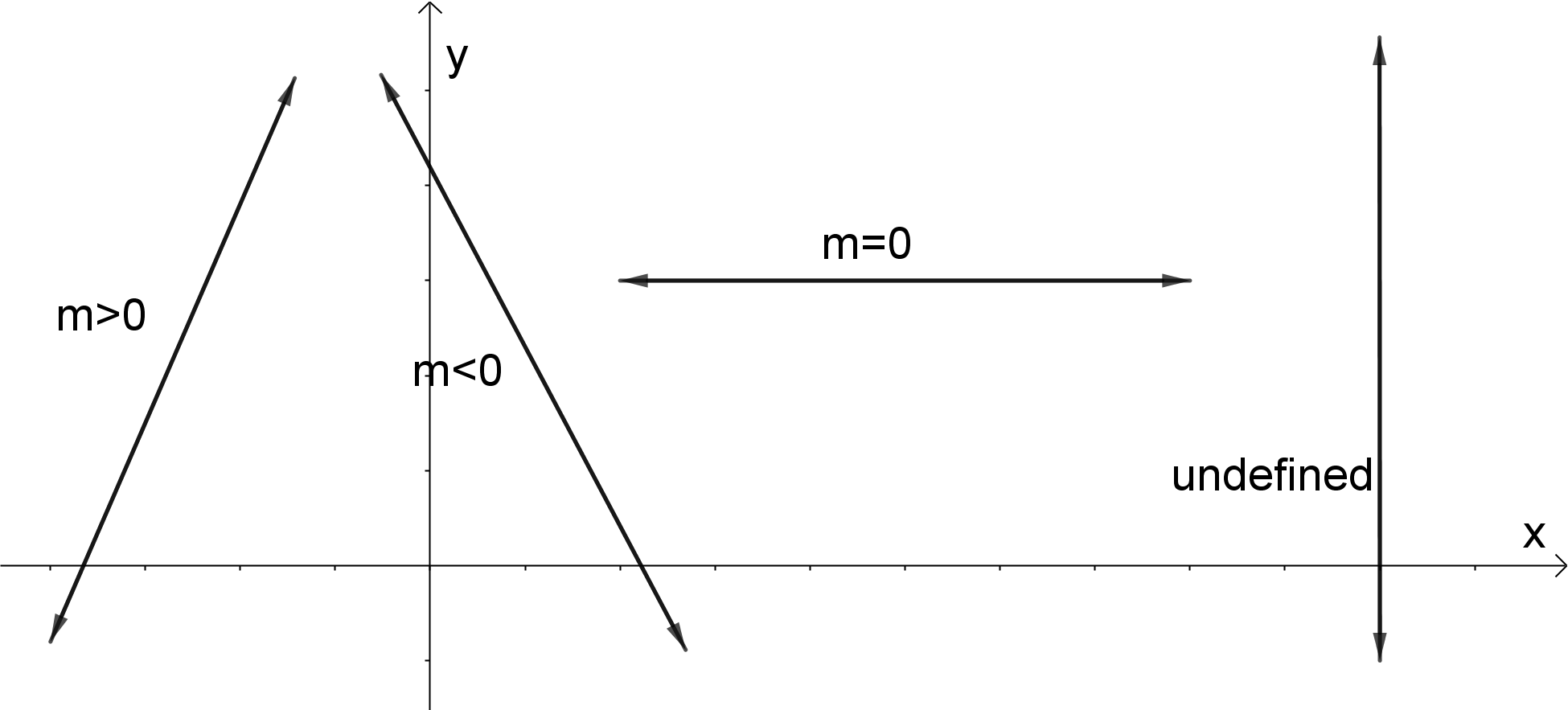
- Positive slope $m>0$, if a line $y=mx+b$ is increasing, i.e. if it goes up from left to right;
- Negative slope $m<0$, if a line $y=mx+b$ is decreasing, i.e. if it goes down from left to right;
- Zero slope, $m=0$, if a line $y=mx+b$ is horizonal. In this case, the equation of the line is$y=b$;
- Undefined slope, if a line $y=mx+b$ is vertical. This is because division by zero leads to infinities. So, the equation of the line is $x=a$. All vertical lines $x=a$ have an infinite or undefined slope.
How to Find Slope?
If we plug in the coordinates $x_A$, $y_A$, $x_B$, $y_B$, into the equation $m=\frac{y_B-y_A}{x_B-x_A}$, we will obtain the slope $m$. In many cases, we can find the slope for a given points by hand, especially for integers. But, if the input values are big real number or number with many decimals, then we should use the slope calculator to get an accurate result.
To find the slope by hand, follow the next steps:
- Insert the coordinates $(x_A,y_A)$ and $(x_B,y_B)$. Let us the formula to calculate the slope of the line passing through the points $(2,5)$ and $(-5, 1)$;
- Subtract the second coordinates and first coordinates, this gives us $y_B-y_A=1-5=-4$ and $x_B-x_A=-5-2=-7$;
- Simplify the fraction to get the slope of $\frac 47$.
Practice Problems for Slope of a Line
The derivative at some point of the curve is the slope of the tangent to the curve at the considering point. Some functions have slopes that may not be the same at every point along the function. Slope tells us the nature of change of function. This nature of change of function is expressed in the sign of the slope. Slopes are very important tool to determine whether two lines perpendicular or not. If the product of slopes of two lines in the plane is $-1$, then the lines are perpendicular and vice-versa. So, the slopes of perpendicular lines are opposite reciprocals.
Practice Problem 1:
Find the slope of the line through $(-1,6)$ and $(-10,15)$.
Practice Problem 2:
The price to rent a car for $12$ days is $\$158$ while for $19$ days is $\$228$. Write a linear equation that model this situation.
The slope calculator, formula, work with steps and practice problems would be very useful for grade school students (K-12 education) to learn about the concept of line in geometry, how to find the general equation of a line and how to find relation between two lines. Many real-world situations can be modeled by linear equations, so the slope calculator can be of great importance of solving such problems.

