Sphere Surface Area & Volume Calculator
Sphere Surface Area & Volume - work with steps
Input Data :
Length = 5 in
Objective :
Find what is volume of the sphere for given input data?
Formula :
Volume = 4πr33
Solution :
Volume = 4 x 3.1416 x 533
= 4 x 3.1416 x 1253
= 1570.79633
Volume = 523.5988 in³
Sphere surface area & volume calculator uses radius length of a sphere, and calculates the surface area and volume of the sphere.
Sphere calculator is an online Geometry tool requires radius length of a sphere. Using this calculator, we will understand methods of how to find the surface area and volume of the sphere.
It is necessary to follow the next steps:
- Enter the radius length of a sphere in the box. The value must be positive real number or parameter. Note that the length of a segment is always positive;
- Press the "GENERATE WORK" button to make the computation;
- Sphere calculator will give the surface area and volume of a sphere.
Output: Two positive real numbers or variables as the surface area and volume of a sphere and corresponding units after that.
Volume of Sphere Formula:
How to Find the Surface Area & Volume of a Sphere?
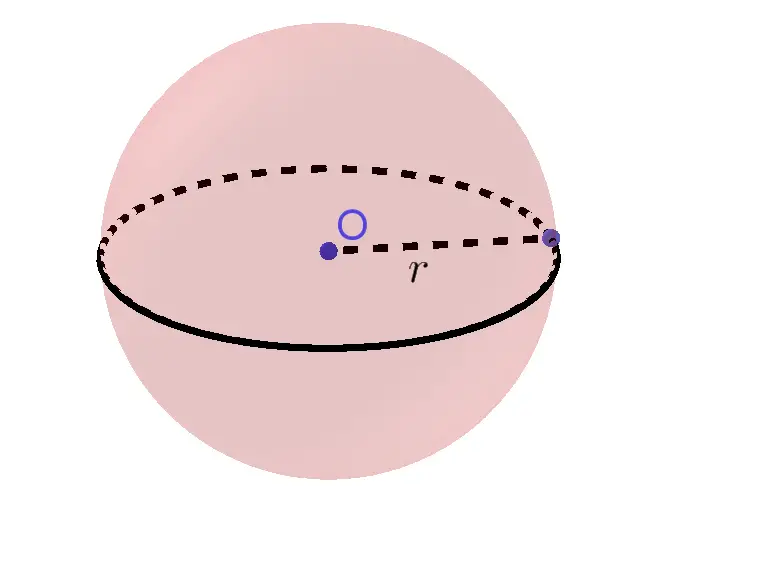
A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere.
The distance from the center of a sphere to any point on the sphere is called the radius of this sphere.
A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the
sphere. All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter. Two spheres of the same radius are congruent.
Any cross section of a sphere by a plane is a circle. The circle obtained as a cross section of the sphere and plane through the center of the sphere is called a great circle. Any plane that passes through the center $O$ of a sphere divides it into two congruent parts well-known as hemispheres.

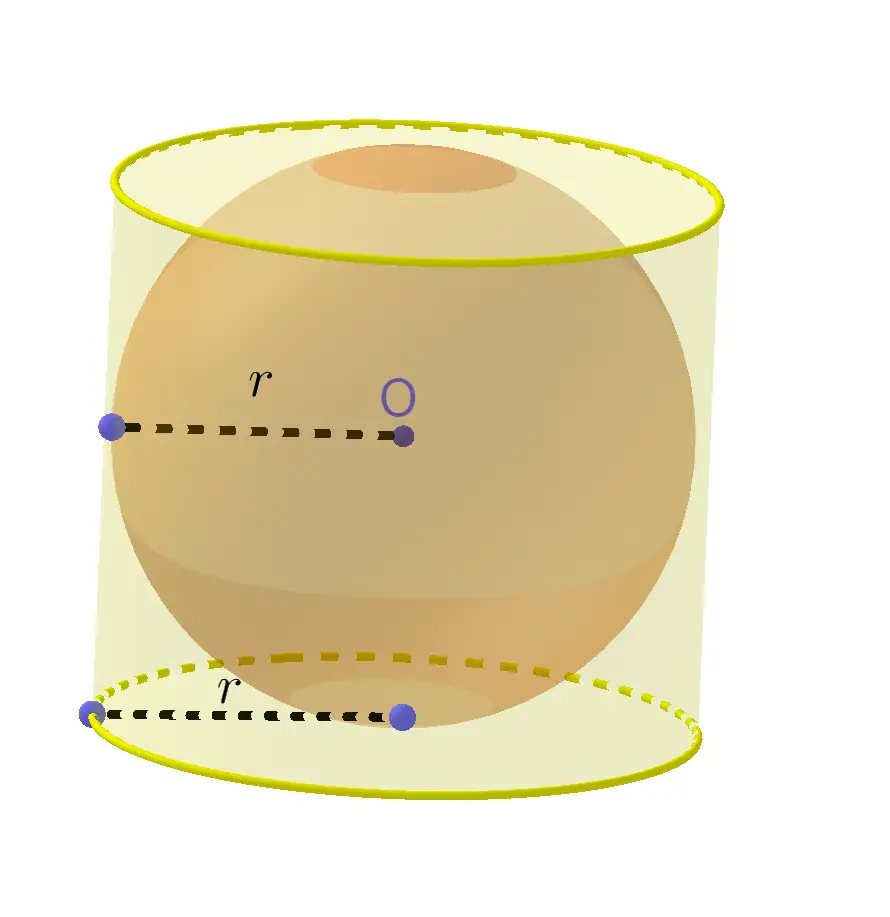
Method for finding volume of a sphere: The volume of each pyramid with a base area of $B$ and a height of $r$ is $\frac 13 B\times h$. The volume $V$ of the sphere can be approximately calculated as volume of $n$ pyramids. Therefore, $$V\approx n\times \frac 13 B\times r=\frac 13(n\times B)\times r\approx \frac 43 r^3\times\pi$$
The Sphere surface area and volume work with steps shows the complete step-by-step calculation for finding the surface area and volume of the sphere with the radius length of $5\;in$ using the surface area and volume formulas. For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button. The grade school students may use this Sphere calculator to generate the work, verify the results of the surface area and volume of the three-dimensional bodies or do their homework problems efficiently. They can use these methods in order to determine the surface area and volume of parts of a sphere.
Real World Problems Using Sphere Metrics
Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations. Hemisphere, spherical segment, spherical wedge, spherical cap and spherical sector are parts of sphere and formulas for their volumes & surface areas are derived by help of the formulas for volume and surface area of sphere.
Many sports that are played with the help of the ball require studying the sphere, as well as its properties. For example, in football, the surface area and volume of a ball is of extreme importance. Different volumes and surface areas of a ball can affect to speed of the kick, trajectory of the ball and its swing in the air.
Apart from football, the surface area and volume of a sphere is important in many other sports as well. Tennis, handball, baseball, golf, basketball all these sports are revolving around the spherical balls.
Volume & Surface Area of Sphere Practice Problems
Practice Problem 1 :
The circumference of Earth at the equator is $24,903$ miles. The diameter of the moon is $2155$ miles. Find the
surface area of Earth and of the moon.
Practice Problem 2 :
If a basketball ball has a diameter of $14$ centimeters and a tennis ball has
a diameter of $7$ centimeters, find the difference between the volumes of the two balls.
The sphere calculator, formula, example calculation (work with steps) and practice problems would be very useful for grade school students of K-12 education to understand the concept of volume & surface area of sphere. This concept can be of significance in geometry, to find the volume & surface area of sphere and its parts. Real life problems on volume & surface area of sphere are very common, so this concept can be of great importance of solving problems.

