Pipe Volume Calculator

Inner Radius

Height

Total Volume = 17.4533ft³

Capacity in liter = 494.221

Capacity in gallon = 14606.5946

GENERATE WORK

Pipe Volume - work with steps

Input Data :
Inner Radius r = 10 in
Height h = 8 ft

Objective :
Find the volume of pipe?

Formula
Volume = πr²h

Solution :
Volume = 3.1416 x 10 x 0.0833333² x 8
= 3.1416 x 0.694443888889 x 8
Volume = 17.4533 ft³

Pipe volume calculator uses inner radius length, outer radius length and height of a cylindrical pipe and calculates the material volume of the pipe and the volume of water or fluid that a pipe can hold. It is an online Geometry tool requires the inner, outer radii and height of a cylindrical pipe. Using this calculator, we will understand methods of how to find the volume of the pipe and the volume of water or fluid in a pipe.
It is necessary to follow the next steps:

Enter the lengths of the inner, outer radii and height of a pipe in the box. These values must be positive real numbers or parameter. Note that the length of a segment is always positive;
Press the "GENERATE WORK" button to make the computation;
Pipe volume calculator will give the volume of the pipe and the volume of water or fluid that a pipe can hold.

Input: Three positive real number or parameter as the inner, outer radii and height of a pipe;
Output: Two positive real numbers or parameters as the volume of the pipe and the volume of water or fluid that a pipe can hold and corresponding units after that.

Pipe Volume Formula :

Volume of Pipe (Radii) Formula:
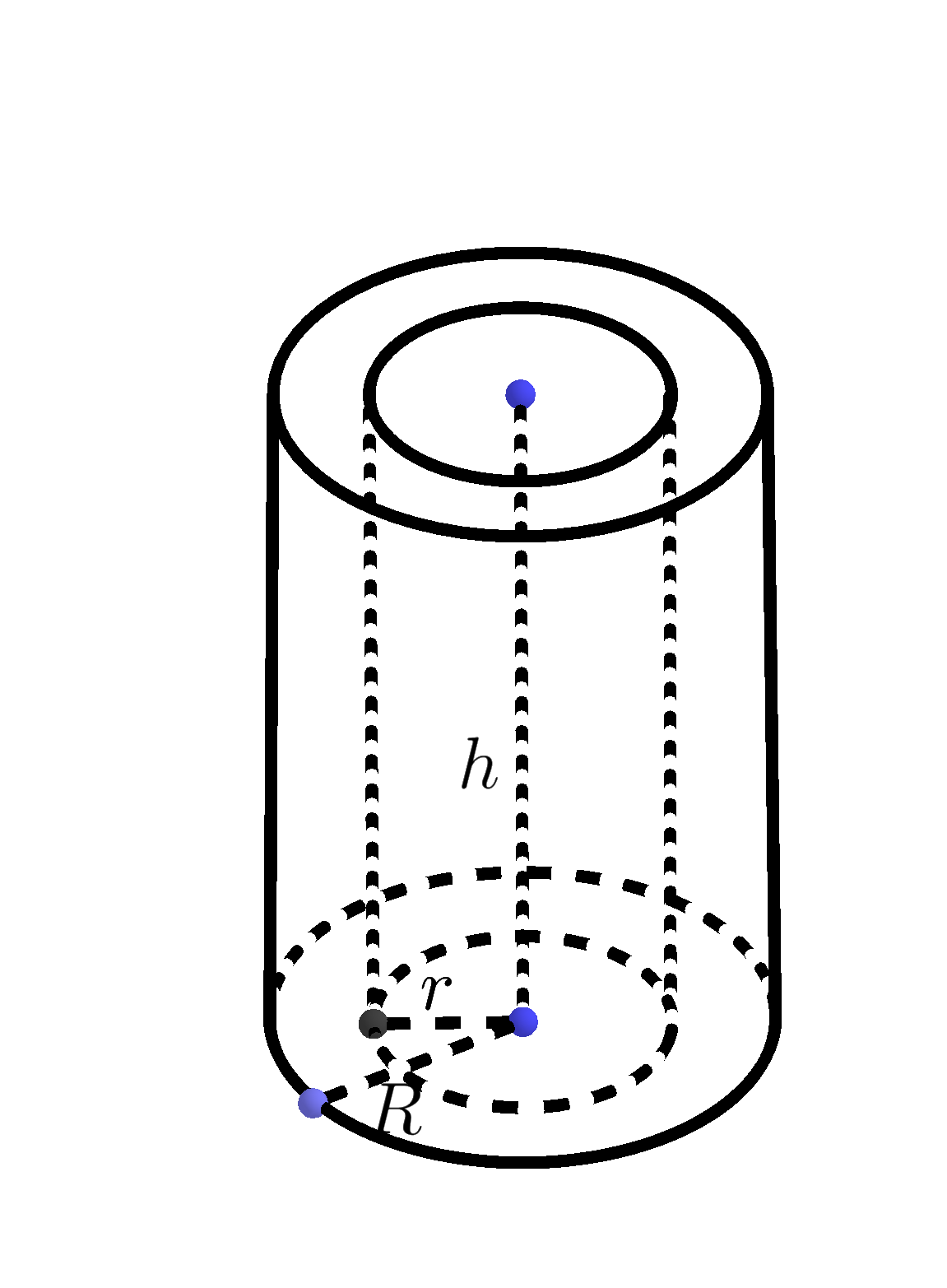
The volume, $V$, of a pipe is determined by the following formula

$$V = (R^2-r^2)\pi \times h,\quad \pi\approx3.14$$

where $R$ is the outer radius length, $r$ is the inner radius length and $h$ is the height of a pipe.

Volume of Pipe (Diameters) Formula:
The volume, $V$, of a pipe is determined by the following formula

$$V = (D^2-d^2)\frac{\pi}{4} \times h \quad \pi\approx3.14$$

where $D$ is the outer diameter length, $d$ is the inner diameter length and $h$ is the height of a pipe.

Volume of Fluid in Pipe Formula:
The volume, $V$, of water or fluid that a pipe can hold is determined by the following formula

$$V = r^2\pi \times h$$

where $r$ is the inner radius length and $h$ is the height of a pipe and $\pi\approx3.14$.

How to Find the Volume of a Pipe?

A cylinder is a three-dimensional solid with congruent bases in a pair of parallel planes. These bases are congruent circles. The axis of the cylinder is the line segment with endpoints at centers of the bases. The height or altitude of a cylinder, denoted by $h$, is the perpendicular distance between its circular bases.
In the following we will consider only the right cylinder, i.e. the cylinder in which the axis and height coincide. A pipe or tube is a hollow cylinder. A hollow cylinder is one which is empty from inside and its base has the inner and outer radius. A hollow cylinder has a base of a ring. Examples of hollow cylinders are: tubes, circular buildings, straws, etc.

The volume of a pipe is the measure of the amount of space that a pipe contributes. In other words, the volume of the material needed to make the pipe. The volume of pipe is the difference between two cylinders. Since the volume of a cylinder is the product of the area of the base and the height, the volume of pipe is

$$V=V_1-V_2=B_1\times h-B_2\times h=(R^2-r^2)\pi \times h$$

Because a diameter of a circle is twice as long as the radius, the previous formula can be expressed in the second way:

$$V=(D^2-d^2)\frac{\pi}{4} \times h$$

where $D$ and $d$ are the outer and inner diameter, respectively.
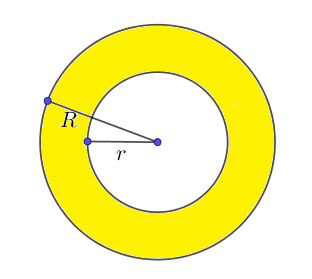
The volume of water or fluid that a pipe can hold (if a pipe is fully filled with it) is equal to the inner volume, the volume of smaller cylinder. So, the volume of water or fluid that a pipe can hold is

$$V_2=B_2\times h=r^2\pi \times h$$

The volume is measured in units such as cube centimeters $(cm^3)$, cube meters $(m^3)$, cube kilometers $(km^3)$ etc.
For example, let us find the volume of water in a pipe if the length of inner radius is $10\;in$ and the height of pipe is $8\;in$. Using the formula for the volume of water that a pipe can hold, we obtain

$$V=r^2\pi \times h=10^2\times\pi\times 8\approx 2513.2741\; in^3$$

The pipe volume work with steps shows the complete step-by-step calculation for finding the volume inside the pipe with the length of its inner radius of $10\;in$ and height of $8\;in$ using the volume formula. For any other values for the base radii and height of a pipe, just supply three positive real numbers and click on the Generate Work button. The grade school students may use this pipe volume calculator to generate the work, verify the results of the volume of the three-dimensional bodies or do their homework problems efficiently.

Real World Problems Using the Volume of a Pipe

The volume of pipe and the volume of water or fluid that a pipe can hold can be useful in many real-life situations. For example, if we want to know the water capacity of the home heating system, or if we want to buy the cylindrical pipe for refilling the swimming pool. So, this calculator is very important for private homeowners, engineers, construction workers, etc.

Pipe Volume Practice Problems

Practice Problem 1:
A copper pipe is $25$ meters long. Its outer and inner diameters are $15$ and $10$ centimeters, respectively. Find the volume of the copper needed to make the pipe.

Practice Problem 2:
The inner diameter of pipe has length of $32$ centimeters and its height is $105$ centimeters. How many liters of water can the pipe hold? ($1000 cm^3=1 l$).

The Pipe Volume calculator, formula, example calculation (work with steps) and practice problems would be very useful for grade school students (K-12 education) to understand the concept of volume of the pipe and cylinder. Real life problems on volume of the pipe and cylinder are very common, so this concept can be of great importance of solving problems.