Hemisphere Calculator

Hemisphere calculator uses radius length of a hemisphere, and calculates the surface area and volume of the hemisphere. Hemisphere calculator is an online Geometry tool requires radius length of a hemisphere. Using this calculator, we will understand methods of how to find the surface area and volume of the hemisphere.

It is necessary to follow the next steps:

1. Enter the radius length of a hemisphere in the box. The value must be positive real number or parameter. Note that the length of a segment is always positive;
2. Press the "GENERATE WORK" button to make the computation;
3. Hemisphere volume and surface area calculator will give the surface area and volume of a hemisphere.

Input: A positive real number or parameter as the radius length of a hemisphere;
Output: Two positive real numbers or variables as the surface area and volume of a hemisphere and corresponding unit after that.

Surface Area of Hemisphere Formula:

How to Find the Surface Area & Volume of a Hemisphere?

A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere. The distance from the center of a sphere to any point on the sphere is called the radius of this sphere. A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere. All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter. Two spheres of the same radius are congruent.

Any cross section of a sphere by a plane is a circle. The circle obtained as a cross section of the sphere and plane through the center of the sphere is called a great circle. Any plane that passes through the center $O$ of a sphere divides it into two congruent parts well-known as hemispheres. The distance from the center of a hemisphere to any point on the hemisphere is called the radius of the hemisphere.

A hemisphere is half of a sphere. To find the surface area, find half of the surface area of the sphere and add the area of the base. The base surface area is a great circle with the same radius as a hemisphere. Therefore, the hemisphere cap area is $\frac 12(4r^2\pi)$ and the base surface area is $r^2\pi$. So, the surface area of hemisphere is the sum of these two areas: $$S=2r^2\pi+r^2\pi=3r^2\pi$$ Method for finding volume of a hemisphere: The volume of each pyramid with a base area of $B$ and a height of $r$ is $\frac 13 B\times h$. The volume $V$ of the sphere can be approximately calculated as volume of $n$ pyramids. Therefore, $$V\approx n\times \frac 13 B\times r=\frac 13(n\times B)\times r\approx \frac 43 r^3\times\pi$$ The sum of two hemispheres volumes is equal to the volume of a sphere. Therefore, the volume of its hemisphere is $$V=\frac 23 r^3\times\pi$$ The surface area of the hemisphere is measured in units such as square centimeters $(cm^2)$, square meters $(m^2)$, square kilometers $(km^2)$, etc. The volume of a hemisphere is measured in units such as cube centimeters $(cm^3)$, cube meters $(m^3)$, cube kilometers $(km^3)$ etc.

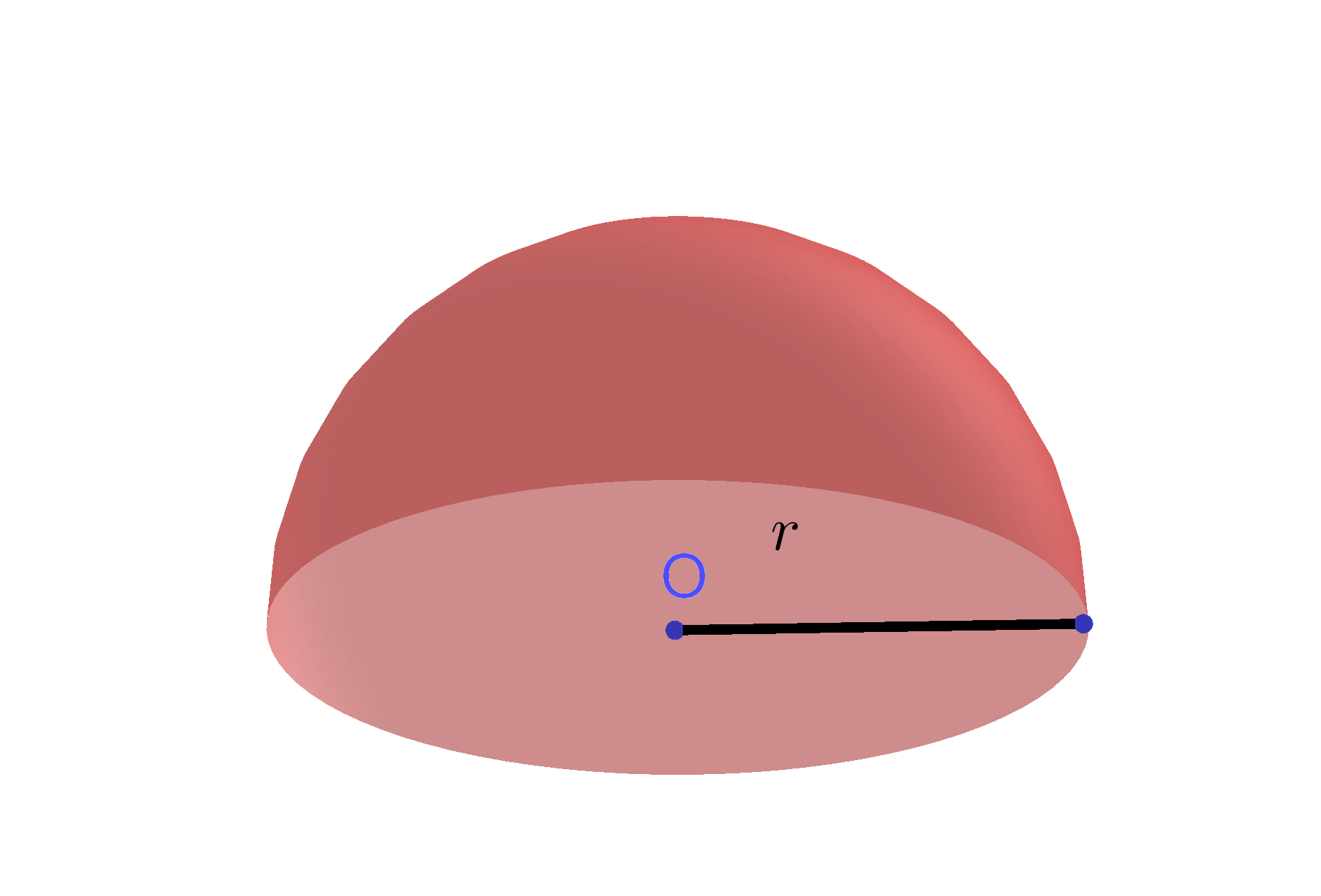
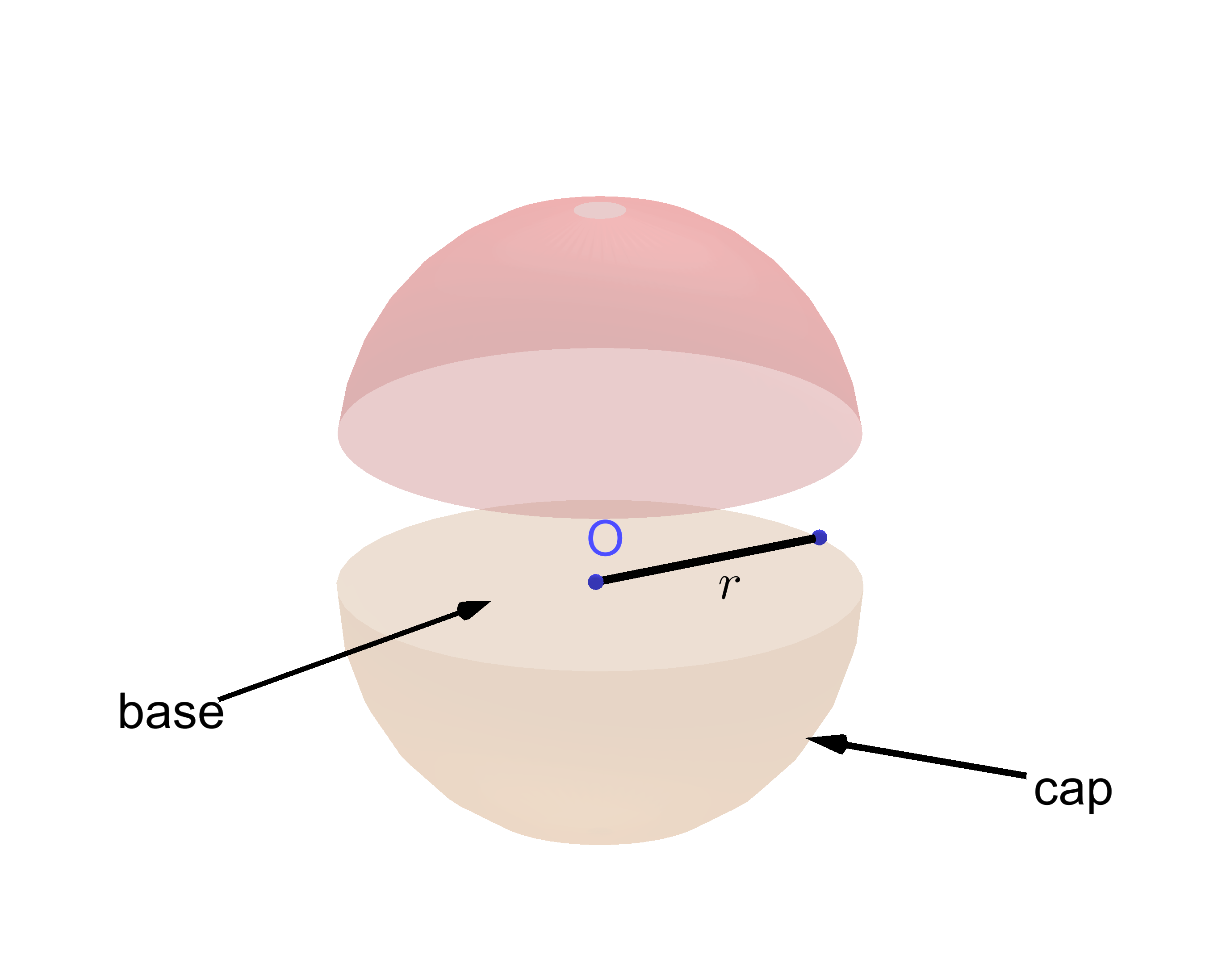
For example, let us find the surface area and volume of a hemisphere with the radius length of $5\;in$. By using the surface area and volume formulas, the surface area and volume of the hemisphere are $$S=3\times 5^2\times\pi,\quad\quad V=\frac 23 5^3\times\pi$$ For $\pi\approx 3.1416$, we obtain $$S=235.62\;in^2,\quad V= 261.7944\; in^3$$ The Hemisphere volume and surface area work with steps shows the complete step-by-step calculation for finding the surface area and volume of the hemisphere with the radius length of $5\;in$ using the hemisphere surface area and volume formulas. For any other value for the length of the radius of a hemisphere, just supply a positive real number and click on the GENERATE WORK button. The grade school students may use this Hemisphere calculator to generate the work, verify the results of the surface area and volume of the three-dimensional bodies or do their homework problems efficiently.

Real World Problems Involves Hemisphere

Many of the objects in nature are shaped as a half of a sphere. For example, the Earth is divided into two hemispheres: northern and southern. An ice cream cone is a combination of a cone and a hemisphere

Hemisphere Practice Problems

Practice Problem 1 :
A hemisphere has a radius of $5$ centimeters. Find the volume of water that can be find in it.

Practice Problem 2 : A hemispherical grill has two racks, both are circular shape. The first rack has a radius of $20$ centimeters, while the second rack has a radius of $15$ inches. Find the difference in the surface areas of hemispheres with bases of these racks.

The hemisphere calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students of K-12 education to understand the concept of volume & surface area of sphere and its part. This concept can be of significance in geometry, to find the volume & surface area of solids, for example a cylinder or cone with hemispherical ends. Real life problems on volume & surface area of hemisphere are very common, so this concept can be of great importance of solving problems.