Volume & Surface Area of Cylinder Calculator
Cylinder Volume & Surface Area - work with steps
Input Data :
Radius = 5 in
Height = 10 in
Objective :
Find the volume of cylinder?
Formula :
Volume = πr2h
Solution :
Volume = 3.1416 x 52 x 10
= 3.1416 x 25 x 10
Volume = 785.3982 in³
Volume & surface area of cylinder calculator uses base radius length and height of a cylinder and calculates the surface area and volume of the cylinder. Cylinder calculator is an online Geometry tool requires base radius length and height of a cylinder. Using this calculator, we will understand methods of how to find the surface area and volume of the cylinder.
It is necessary to follow the next steps:
- Enter the base radius length and height of a cylinder in the box. These values must be positive real numbers or parameter. Note that the length of a segment is always positive;
- Press the "GENERATE WORK" button to make the computation;
- Cylinder calculator will give the surface area and volume of a cylinder.
Output : Two positive real numbers or variables as the surface area and volume of a cylinder and corresponding units after that.
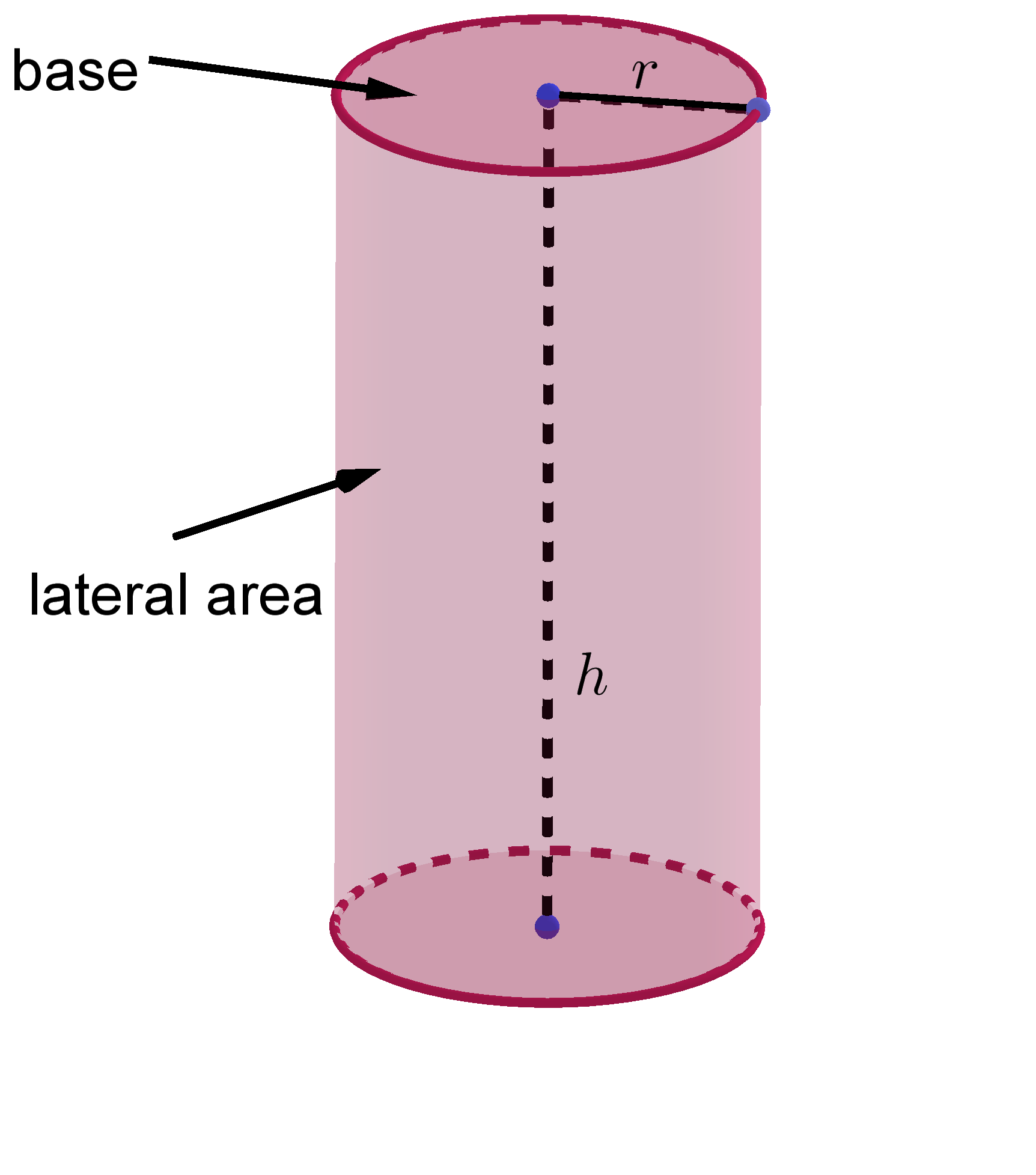
The surface area, $S$, of a cylinder is determined by the following formula $$S = 2\pi r(h+r)$$ where $r$ is the base radius length, $h$ is the height of a cylinder and $\pi\approx3.14$.
Volume of Cylinder Formula:
The volume, $V$, of a cylinder is determined by the following formula $$V = r^2\pi \times h$$ where $r$ is the base radius length, $h$ is the height of a cylinder and $\pi\approx3.14$.
How to Find the Volume & Surface Area of a Cylinder?
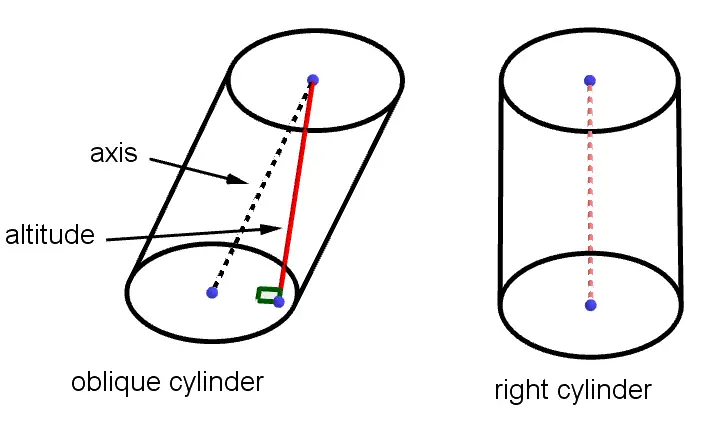
A cylinder is a three-dimensional solid with congruent bases in a pair of parallel planes. These bases are congruent circles. The axis of the cylinder is the line segment with endpoints at centers of the bases.
The height or altitude of a cylinder, denoted by $h$, is the perpendicular distance between its circular bases.There are two types of cylinder:
- Right Cylinder;
- Oblique Cylinder.
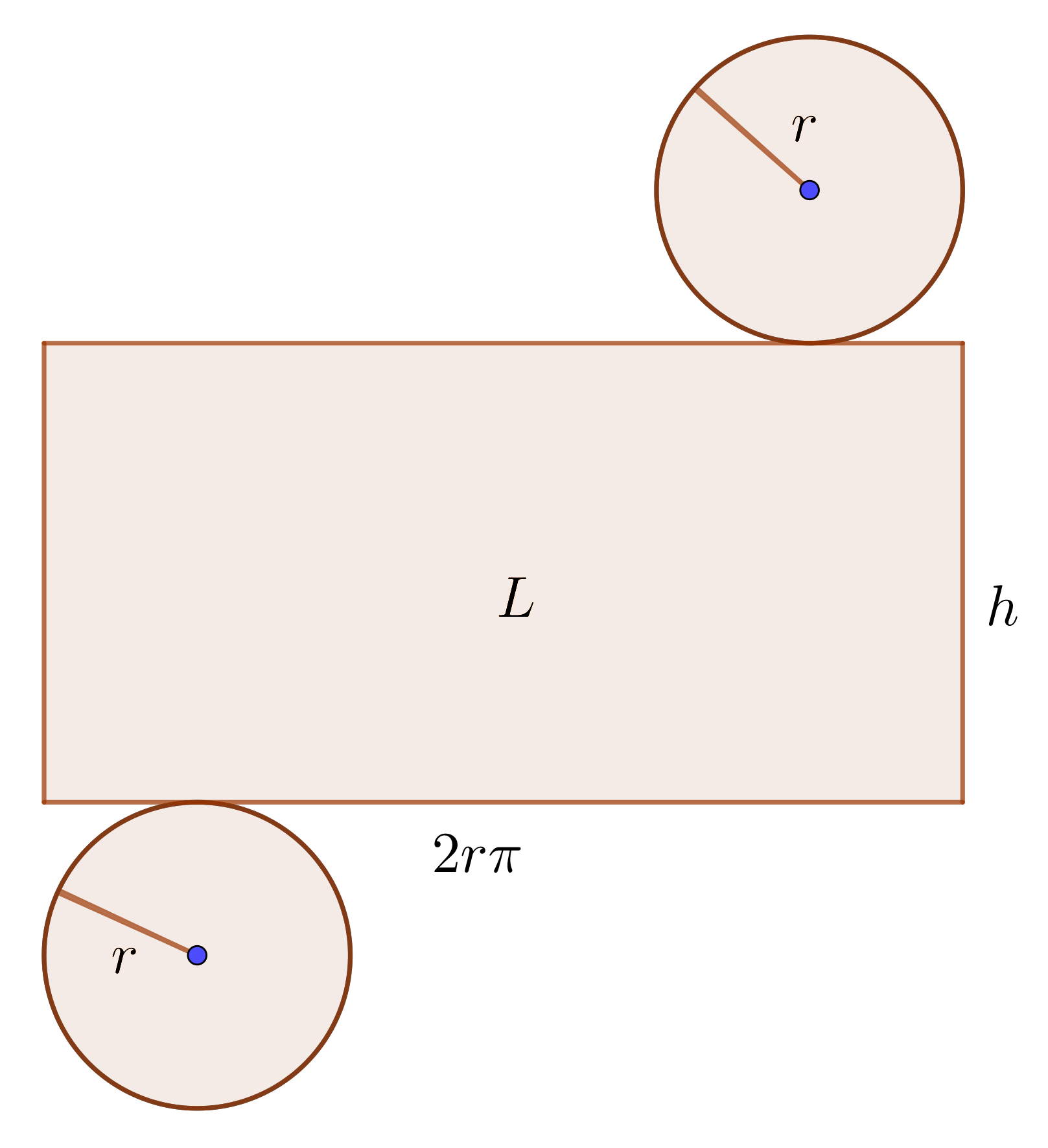
The surface area of the cylinder is measured in units such as square centimeters $(cm^2)$, square meters $(m^2)$, square kilometers $(km^2)$, etc. The volume of a cylinder is measured in units such as cube centimeters $(cm^3)$, cube meters $(m^3)$, cube kilometers $(km^3)$ etc.
The cylinder volume & surface area work with steps shows the complete step-by-step calculation for finding the surface area and volume of the cylinder with the length of its base radius of $5\;in$ and height of $10\;in$ using the surface area and volume formulas. For any other values for the base radius lengths and height of a cylinder, just supply two positive real numbers and click on the Generate Work button. The grade school students may use this cylinder calculator to generate the work, verify the results of the surface area and volume of the three-dimensional bodies or do their homework problems efficiently.
Real World Problems Using Cylinder Metrics
Calculating volume and surface area of cylinder play an important role in mathematics and real life as well. Formulas for volume & surface area of a cylinder can be used to find formulas for volume & surface area of the pipe. A knowledge of surface area formula is useful to calculate how much material we need to make some cylindrical shapes. The volume of cylinder formula is useful in determining the capacity of cylindrical shapes. For example, to design or find the capacity of a water tank, containers, bottle, cylindrical flasks, etc. With volume formula, we can better understand the density and capacity problems.
Cylinder Practice Problems
Practice Problem 1:
Find the base radius length of a right cylinder if the surface area is $256$ square
meters and the height is $18$ meters.
Practice Problem 2:
Silo has a cylindrical shape. Find the lateral area of a silo $20$ meters tall with the base radius length of $5$ meters.
A second silo is $30$ meters tall. If both silos have the same lateral area, find the radius length of the second silo.
Practice Problem 3:
An Aquarium has cylindrical tanks. If the tank holds $100,000$ liters and is $5$ meter deep. Find the radius of the tank.
The cylinder calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the concept of volume & surface area of the cylinder. This concept can be of significance in geometry, to find the volume & surface area of cylinder and pipe. Real life problems on volume & surface area of the cylinder are very common, so this concept can be of great importance of solving problems.

