Prime or Composite Calculator
Composite or Prime Number calculator determines whether a number is prime or composite. If it is composite the calculator finds all of the factors of the composite number using the prime factorization. This calculator is closely connected with the prime factors of a number calculator.
It is necessary to follow the next steps:
- Enter a number in the box. The number must be positive integer;
- Press the "CALCULATE" button to make the computation;
- Prime number calculator determines if a given number is prime or composite.
Output : The appropriate message, "The number is a Prime Number" if the number is a prime, otherwise "The number is not a Prime Number".
What is Prime Number?
A prime number is a natural number greater than `1` that has exactly two factors, `1` and itself. Negative integers cannot be prime. A composite number is any positive integer that is not prime. Zero and 1 are neither prime nor composite numbers. For instance, `4, 6, 8, 9, 10, 12, 14`, etc are the examples of a composite number. In the table below, we manually check which number is prime
| Natural numbers | Factors | Prime/Composite |
|---|---|---|
| 1 | 1 | / |
| 2 | 1,2 | Prime |
| 3 | 1,3 | Prime |
| 4 | 1,2,4 | Composite |
| 5 | 1,5 | Prime |
| 6 | 1,2,3,6 | Composite |
| 7 | 1,7 | Prime |
| 8 | 1,2,4,8 | Composite |
| 9 | 1,3,9 | Composite |
Two integers are relatively prime, if the only positive integer that divides both of them is `1`. So, any prime number that divides one of them does not divide the other. In the following we give some interesting fact about prime numbers:
- The number `2` is the only even prime number;
- Every prime number greater $3$ can be represented as $6n+1$ or $6n-1$, where $n$ is natural number;
- The numbers `2` and `3` are only two consecutive natural numbers which are relatively prime;
- Goldbach's conjecture: Every even integer greater than `2` can be expressed as the sum of two primes.problem is one of the oldest unsolved problems in number theory.
- Fermat's Little Theorem: If $n$ is a prime number, then for any integer `a`, the number $a^n - a$ is an integer multiple of `n`.
How to Find Prime Number?
There are some methods for determining if a number $n$ is prime:
- Rectangular method. This method is useful for small numbers. For example, let us determine if the number $15$ is prime or not. We draw as many different rectangular arrangements of $15$ squares as possible. Because numbers of squares can be arranged in more than one way, the number $15$ is not a prime number.
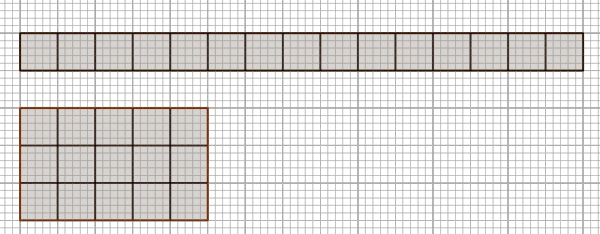
- School method. Check if all numbers from $2$ to $n-1$ divides $n$. If we find any number that divides, then the number $n$ is not prime; Below is the implementation of this method.;
- Optimized school method. Instead of checking all numbers from $2$ to $n-1$, we can check all numbers from $2$ to $\sqrt{n}$ because a larger factor of $n$ must be a multiple of smaller factor that has been already checked;
- Fermat Method. This method is based on Fermat's Little Theorem, etc.
Practice Problems to Find Prime or Composite
Prime numbers play an important role in cryptography. All integer numbers (except 0 and 1) are made up of primes. RSA (Rivest-Shamir-Adleman) is one of the first public-key
cryptosystems and it is widely used for secure information. RSA is one of the basic cryptographic algorithms. Basically, a public key consists of a product of two large primes used to encrypt
a message and a secret key consists of those two primes used to decrypt the message (for more, refer to (cryptosystem)).
In nature, the prime numbers are widespread. For instance, cicadas have reproductive cycles that are $13$ or $17$ years long. The reason is to minimize the frequency with which their reproduction coincides with another organism. These other organisms may be, for example, predators or competitors for the same food which would be at a premium when
reproducing.
Practice Problem 1:
Determine whether the number `391` is prime or composite.
Practice Problem 2:
A group of $137$ children is on the soccer camp. The children will be arranged in rows with the same number of children in each row. Is it possible?
Practice Problem 3:
Find two prime numbers `A` and $B$ less than `60`, if the arithmetic mean of these numbers is also a prime number.
The prime number calculator, methods, example calculation and practice problems would be very useful for grade school students of K-12 education to learn how to determine whether the given number is prime or composite. Users can use this concept in number theory problems as well as in computer science.

