3x3 Matrix Subtraction Calculator
3x3 matrix subtraction calculatoruses two $3\times 3$ matrices $A$ and $B$ and calculates difference between $A$
and $B$. It is an online math tool specially programmed to perform matrix subtraction between the two $3\times 3$ matrices $A$ and $B$.
It is necessary to follow the next steps:
- Press the "GENERATE WORK" button to make the computation;
- 3x3 matrix subtraction calculator will give the difference between the first matrix and the second matrix.
Output: A $3\times3$ matrix.
$3\times 3$ Matrix Subtraction Formula:
What is Matrix?
Matrices are a powerful tool in mathematics, science and life. Matrices are everywhere and they have significant applications. For example, spreadsheet such as Excel or written a table represents a matrix. The word "matrix" is the Latin word and it means "womb". This term was introduced by J. J. Sylvester (English mathematician) in 1850.
The first need for matrices was in the studying of systems of simultaneous linear equations.
A matrix is a rectangular array of numbers, arranged in the following way
$$A=\left(
\begin{array}{cccc}
a_{11} & a_{12} & \ldots&a_{1n} \\
a_{21} & a_{22} & \ldots& a_{2n} \\
\ldots &\ldots &\ldots&\ldots\\
a_{m1} & a_{m2} & \ldots&a_{mn} \\
\end{array}
\right)=\left[
\begin{array}{cccc}
a_{11} & a_{12} & \ldots&a_{1n} \\
a_{21} & a_{22} & \ldots& a_{2n} \\
\ldots &\ldots &\ldots&\ldots\\
a_{m1} & a_{m2} & \ldots&a_{mn} \\
\end{array}
\right]$$
There are two notation of matrix: in parentheses or box brackets. The terms in the matrix are called its entries or its elements.
Matrices are most often denoted by upper-case letters, while the corresponding lower-case letters, with two subscript indices, are the elements of matrices.
For examples, matrices are denoted by $A,B,\ldots Z$ and its elements by $a_{11}$ or $a_{1,1}$, etc. The horizontal and vertical lines of entries in a matrix are called rows and columns, respectively.
The size of a matrix is a Descartes product of the number of rows and columns that it contains. A matrix with $m$ rows and $n$ columns is called an $m\times n$ matrix. In this case $m$ and $n$ are its dimensions. If a matrix consists of only one row, it is called a row matrix. If a matrix consists only one column is called a column matrix. A matrix which contains only zeros as elements is called a zero matrix.
How to Find the Difference between Two 3x3 Matrices?
Matrices $A$ and $B$ can be subtracted if and only if their sizes are equal. Such matrices are called commensurate for addition or
subtraction. The difference $A-B$ of two $m\times n$ matrices is equal to the sum $A + (-B)$,
where $-B$ represents the additive inverse of the matrix $B$. So, the difference a matrix $C=A-B$ with elements
$$c_{ij}=a_{ij}+(-b_{ij})=a_{ij}-b_{ij}$$
The matrix $C$ has the same size as the matrices $A$ and $B$.
This means, each element in $C$ is equal to the difference between the elements of $A$ and $B$ that are located in corresponding places. For example,
$c_{13}=a_{13}-b_{13}$. If two matrices have different sizes, their difference is not defined.
The subtraction of matrices is non-commutative operation, i.e $A-B\ne B-A$. Subtracting two matrices is very similar to adding matrices with the only difference being subtracting corresponding elements.
A $3\times 3$ matrix has $3$ columns and $3$ rows. For example, the difference between two $3\times 3$ matrices $A$ and $B$ is a matrix $C$ such that
$$\begin{align} C=&\left(
\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{array}
\right)-
\left(
\begin{array}{ccc}
b_{11} & b_{12} & b_{13} \\
b_{21} & b_{22} & b_{23} \\
b_{31} &b_{32} & b_{33} \\
\end{array}
\right)= \left(\begin{array}{ccc}
a_{11}-b_{11}& a_{12}-b_{12}& a_{13}-b_{13} \\
a_{21}-b_{21} &a_{22}-b_{22}& a_{23}-b_{23}\\
a_{31}-b_{31} &a_{32}-b_{32} & a_{33}-b_{33} \\
\end{array}\right)\end{align}$$
For example, let us find the difference $A-B$ for
$$A=\left(
\begin{array}{ccc}
10 & 20 & 10 \\
4 & 5 & 6 \\
2 & 3 & 5 \\
\end{array}
\right)\quad\mbox{and}\quad B=\left(
\begin{array}{ccc}
3 & 2 & 4 \\
3 & 3 & 9 \\
4 & 4 & 2 \\
\end{array}
\right)$$
Using the matrix subtraction formula, the difference between the matrices $A$ and $B$ is the matrix
$$A-B=\left(
\begin{array}{ccc}
10-3 & 20-2 & 10-4 \\
4-3 & 5-3 & 6-9 \\
2-4 & 3-4 & 5-2 \\
\end{array}
\right)=\left(
\begin{array}{ccc}
7 & 18 & 6 \\
1 & 2 & -3 \\
-2 & -1 & 3 \\
\end{array}
\right)$$
The $3\times 3$ matrix subtraction work with steps shows the complete step-by-step calculation for
finding the difference of two $3\times3$ matrices $A$ and $B$ using the matrix subtraction formula. For
any other matrices, just supply elements of $2$ matrices in terms of a real numbers and click on the Generate Work
button. The grade school students may use this 3x3 matrix subtraction calculator to generate the
work, verify the results of subtracting matrices derived by hand, or do their homework problems efficiently.
Real World Problems Using 3x3 Matrix Subtraction
Matrices are applied in many subjects beyond mathematics. For example, designing computer game graphics, 3D geometry and visualization, social networks, representing real world data, economics, robotics and automation, etc.
Matrix Subtraction Practice Problems
Practice Problem 1 :
Find the difference between the matrices $$C=\left(
\begin{array}{ccc}
3.8 & 9 & 1.9 \\
0 & 1.5 & -6.6 \\
12 & -9.7 & 5 \\
\end{array}
\right)\quad\mbox{and}\quad D=\left(
\begin{array}{ccc}
2.8 & 0 & 4.1 \\
3 & -7.6 & 0 \\
5 & 8.4 & 2 \\
\end{array}
\right)$$
Practice Problem 2 :
The following two matrices represent studies to find what types of sports are most popular and how they could attract more people. Data are given in percent.
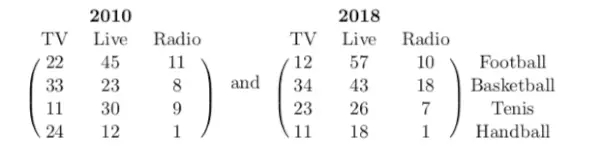
The 3x3 matrix subtraction calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the subtraction of two or more matrices. They can use matrix subtraction to model and solve real-life problems.

