nxn Matrix Determinant Calculator

nxn matrix determinant calculator calculates a determinant of a matrix with real elements. It is an online tool programmed to calculate the determinant value of the given matrix input elements. This calculator is designed to calculate $2\times 2$, $3\times3$ and $4\times 4$ matrix determinant value. Select the appropriate calculator from the list of three.

It is necessary to follow the next steps:

1. Enter elements of matrix in the box. Elements of matrices must be real numbers.
2. Press the "GENERATE WORK" button to make the computation;
3. nxn matrix determinant calculator will give the real value that represents useful information about the matrix.

Input: A matrix with real elements;
Output: Real number.

$2\times 2$ Matrix Multiplication Formula:

$3\times 3$ Matrix Multiplication Formula:

$4\times 4$ Matrix Multiplication Formula:

What is Matrix Determinant?

The concept of the matrix determinant appeared in Germany and Japan at almost identical times. Seki wrote about it first in 1683 with his Method of Solving the Dissimulated Problems. Seki developed the pattern for determinants for $2 \times 2$, $3 \times 3$, $4 \times 4$, and $5 \times 5$ matrices and used them to solve equations. In the same year, G. Leibniz wrote about a method for solving a system of equations. This method is well known as Cramers Rule. The determinant of a square matrix $A$ is an unique, real number which is an attribute of the matrix $A$. The determinant of the matrix $A$ is denoted by $det(A)$ or $|A|$.

How to Find Matrix Determinant?

Let us consider the matrix $A=\left[ \begin{array}{cc} a &b\\ c& d \\ \end{array} \right]$ of the size $2\times2$. The real number $$\left|\begin{array}{cc} a &b\\ c& d \\ \end{array} \right|=ad-cb$$ is the determinant of the matrix $A$. More precisely, to find a $2\times 2$ matrix determinant we need to follow next steps:

• Multiply the element in the first row and first column by the elements in the second row and second column;
• Multiply the element in the first row and second column by the element in the second row and first column;
• $2\times 2$ matrix determinant is the difference between the second product and the first product.

The minor of an element of any $n\times n$ matrix determinant is a $(n-1)\times (n-1)$ matrix determinant. If we delete the row and column containing the element, then we get appropriate minor. For example, the minor of the element $a$, element in the first row and first column, of the determinant To evaluate an $n\times n$ matrix determinant we need to expand the determinant by minors. Firstly, we choose a row in the matrix. At each position in the row, we multiply the element times its minor times its position sign, and add all sums for the whole row. The position signs in a matrix are plus or minus depending on the position of element. For instance, the position signs in $3\times 3$ matrix are $$\left[ \begin{array}{ccc} + & - & + \\ -& + & - \\ + & - & + \\ \end{array} \right]$$ This means, $$\begin{align} det(A)=|A|&=\left| \begin{array}{ccc} a & b & c \\ d& e & f \\ g & h & i \\ \end{array} \right| \\&=a\left| \begin{array}{cc} e &f \\ h & i \\ \end{array} \right|-b\left| \begin{array}{cc} d &f \\ g & i \\ \end{array} \right|+c\left| \begin{array}{cc} d &e \\ g & h \\ \end{array} \right|\end{align}$$ If we apply this method for computing of a $4\times 4$ determinant, we obtain $$\begin{align} det(A)=|A|&=\left| \begin{array}{cccc} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \\ \end{array} \right| \\&=a\left| \begin{array}{ccc} f & g & h \\ j & k & l \\ n & o & p \\ \end{array} \right|-b\left| \begin{array}{ccc} e & g & h \\ i & k & l \\ m & o & p \\ \end{array} \right|+c\left| \begin{array}{ccc} e & f & h \\ i & j & l \\ m & n & p \\ \end{array} \right|-d\left| \begin{array}{ccc} e & f & g \\ i & j & k \\ m & n & o \\ \end{array} \right| \end{align}$$ For each element in the original matrix, its minor is a $3\times 3$ determinant.

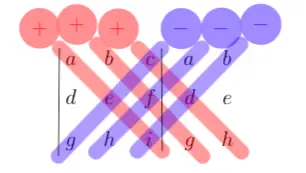
There is another way for computing of a $3\times 3$ determinant well knows as Sarrus' rule or Sarrus' scheme.

• Extend the determinant by rewriting the first two columns of numbers:
• Add the products of the red diagonals and subtract the products of the blue diagonals, i.e. $$det(A)=aei+bfg+cdh-ceg-afh-bdi$$ This rule can be remembered by remembering about diagonals of the extended determinant read diagonals means plus $(aei+bfg+cdh)$ and blue diagonals means minus $(-ceg-afh-bdi)$.

Sarrus's rule can not be applied for computing of a $4\times 4$ determinant, it requires some modifications. For example, let us find the determinant of the $3\times 3$ matrix $$\left|\begin{array}{ccc} 10 & 20 & 10 \\ 4& 5 & 6 \\ 2 &3 & 5 \\ \end{array} \right|$$ Using the Sarrus' rule, we get $$\left|\begin{array}{ccc|cc} 10 & 20 & 10&10 & 20 \\ 4& 5 & 6&4& 5 \\ 2 &3 & 5&2&3 \\ \end{array} \right.=10\cdot5\cdot5+20\cdot6\cdot2+10\cdot4\cdot 3-10\cdot5\cdot2-10\cdot6\cdot3-20\cdot4\cdot5=-70$$ The $n\times n$ Matrix Determinant work with steps shows the complete step-by-step calculation for finding a determinant of $3\times 3$ matrix $A$ using the determinant formula. For any other matrices, just supply real numbers as elements of matrix and click on the GENERATE WORK button. The grade school students and people who study math use this nxn matrix determinant calculator to generate the work, verify the results of matrix determinant derived by hand, or do their homework problems efficiently. The grade school students can also use this calculator for solving system of linear equations.

Real World Problems Using Matrix Determinant

Geometrically, determinant represents the volume of $n$-dimensional parallelepiped spanned by the column or row vectors of the matrix. The vector product and the scalar product are the two ways of multiplying vectors which are applicable in almost all field of sciences. If the vectors are expressed in terms of unit vectors $\vec i, \vec j,$ and $\vec k$ in the $x, y,$ and $z$ directions, then the vector product of two vectors $\vec a=(x_a,y_a,z_a)$ and $\vec b=(x_b,y_b,z_b)$ is $$\left|\begin{array}{ccc} \vec i & \vec j &\vec k \\ x_a& x_b & x_c \\ y_a &y_b & y_c \\ \end{array} \right|$$ Determinant can be used to calculate areas of parallelogram sand triangles on the coordinate plane. For instance, the area of triangle $\Delta ABC$ with $A(x_A,y_A)$, $B(x_B,y_B)$ and $C(x_C,y_C)$ is determined by the formula $$A(\Delta ABC)=\frac12|\left|\begin{array}{ccc} x_A & y_A &1 \\ x_B& y_B & 1 \\ x_C &y_C & 1 \\ \end{array} \right| |$$ Another important application of matrix determinant is in solving systems of linear equations, so called Cramer's Rule. The determinant informs us whether the system has a unique solution. Determinant may also be useful in finding the inverse of a nonsingular matrix, etc.

Matrix Determinant Practice Problems

Practice Problem 1 :
Find the vector product of the vectors $\vec a=(1,-3,0)$ and $\vec b=(3,5,7).$

Practice Problem 2 :
Given the triangle $\Delta ABC$ with $A(0,0)$, $B(3,4)$ and $C(-2,5)$. Using the determinant find the area of the triangle $\Delta ABC$.

The nxn matrix determinant calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the concept of matrix determinant. This concept is conceived in almost all areas of science, so it will be helpful in solving more complex problems.